首先声明一些符号:
- 模型参数量:$\Phi$
- GPU数量:$N$(有时候可能误写成了$n$)
- Pipeline degree(或者说PP size):$p$
- TP size:$t$
除非特殊声明,某些未说明的符号可能遵循LLM时代的transformer参数量、计算量、激活值的分析的符号表示。
数据并行
传统数据并行DP
使用场景:每张卡上都有一份完整的模型(因此模型不会太大),通常单机多卡(比如单机八卡进行数据并行)
具体方法:基本使用参数服务器的编程框架,
最基本的范式为:
将一个batch分成若干份mini-batch,每个worker上进行一份mini-batch的计算(前向和反向),得到一份模型参数的梯度
AllReduce梯度:每个worker将梯度push到Server上,Server对梯度进行reduce(或者说求平均),再boardcast给每个worker
Server即称为参数服务器,可以是GPU,也可以是CPU,也可以是多张GPU/CPU。如果是CPU,则通过PCIe通信,慢;如果是GPU,则通过Nvlink通信,更快;如果Server是多张GPU/CPU,则Server之间也要进行通信
每个worker更新参数
在第一步得到worker上自己的梯度之后,更新梯度有两种方式: 第一种方式就是上面的,AllReduce梯度后,每个worker得到平均后的梯度,然后每个worker再更新参数(下面的DDP也是这种方式) 第二种方式是,每个worker的梯度push到Server上,Server同样对梯度取平均,并且Server上也有一份模型参数,Server对这份模型参数进行更新,最后将更新后的参数boardcast给每个worker。这种方式明显对Server压力更大(原来只要allreduce梯度,现在还要自己有一份模型参数,还有更新参数),但是worker就省了更新参数。
另一种参数服务器的范式为:每个GPU都是参数服务器,比如说GPU1负责w1的AllReduce,GPU2负责w2的AllReduce,…
缺点:
每张卡上都要存储一份完整的模型,而且没法与其他并行方式组合使用
通讯开销大,因为push和boardcast传输的都是一份完整的参数的梯度
- 每次迭代,每个Worker(共N-1个)push的通讯量为$\Phi$,Server总通讯量(boardcast)为$(N-1)\Phi$,所以更大的问题在于通讯负载不均,系统总通讯量为$(N-1)\Phi + (N-1)\Phi = 2(N-1)\Phi \approx 2N\Phi$(与DDP相同)
Server进行allreduce的过程中,其他所有worker都在等待
针对这一点,某些框架提出了一些异步的解决方法,但其实都是一个效果与性能的tradeoff,比如参数服务器中3.4节提到了 Asynchronous Tasks and Dependency(其实我没太看懂),这篇博客图解大模型训练之:数据并行上篇(DP, DDP与ZeRO)中对这一部分进行了说明,文中叫做“梯度异步更新”,比如在延迟为1的异步更新中,下面重新画一下示意图(这里是针对某一个worker进行示意)。其实感觉就是梯度累计的意思(这篇博客中也简要提到了梯度累计,搜索"gradient accumulation")
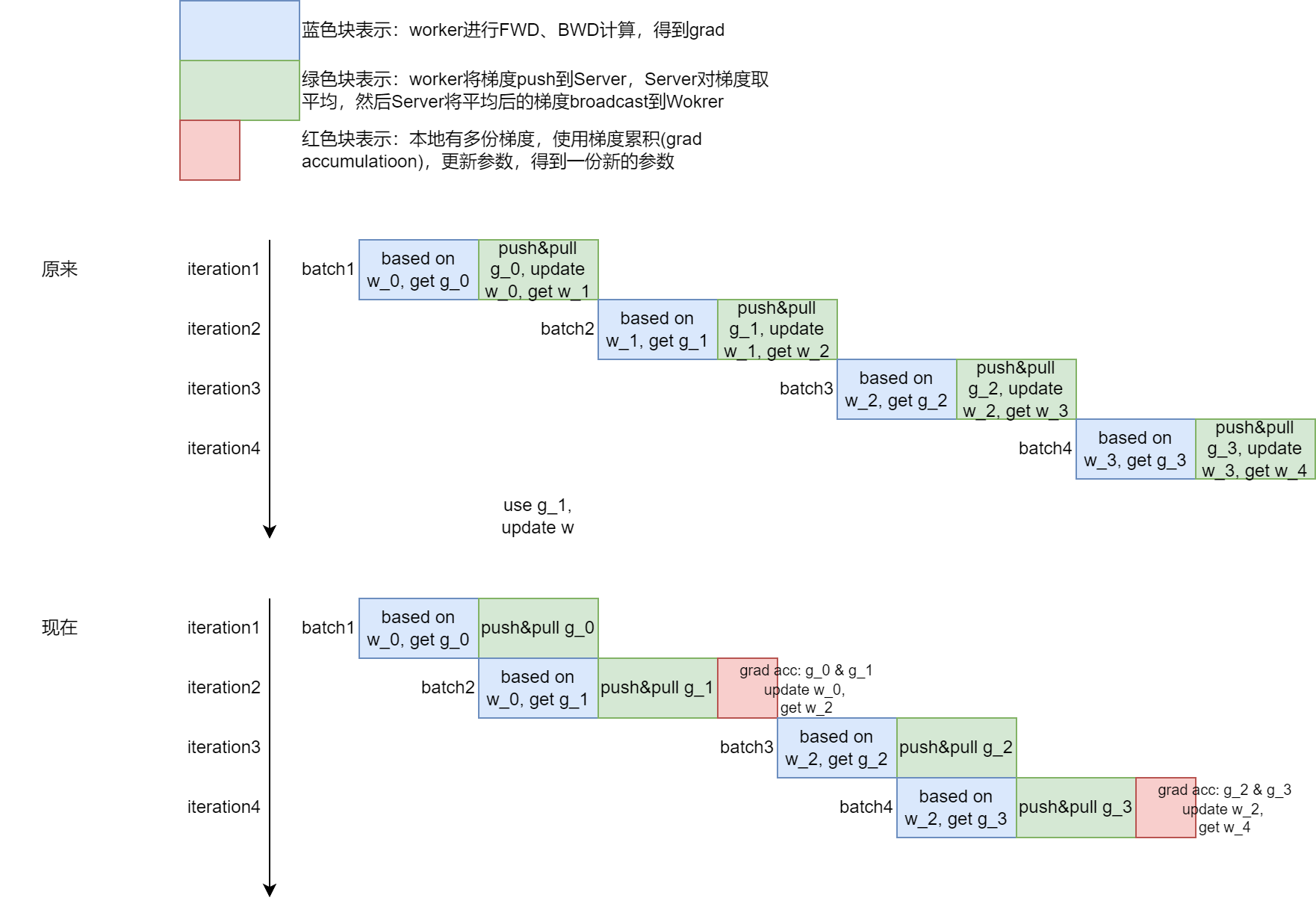
分布式数据并行DDP
使用场景:每张卡上都有一份完整的模型,常用于多机多卡
具体方法:
将一个batch分成若干份mini-batch,每个worker上进行一份mini-batch的计算(前向和反向),得到一份模型的梯度
使用Ring-AllReduce,使得每个Worker都得到一份完整的reduced梯度(聚合后的梯度)
有几个关键词需要注意:一份完整的/一块不完整的,reduced/un-reduced,完整是指tensor没有切开,reduced是指多个tensor经过allreduce聚合
- 一开始每个Worker只有自己的一份完整的un-reduced梯度,而且将梯度分成N块
- Reduce-Scatter:每次每个Worker向相邻的下一个Worker发送一块不完整的un-reduced梯度(大小是$\frac{\Phi}{N}$,进行一次reduce),一共N-1次,通讯量$(N-1)\times \frac{\Phi}{N}$,此时每个Worker都有一块不完整的reduced梯度
- All-Gather:每次每个Worker向相邻的下一个Worker发送一块不完整的reduced梯度(大小是$\frac{\Phi}{N}$,直接进行替换),一共N-1次,通讯量$(N-1)\times \frac{\Phi}{N}$,此时每个Worker都有一份完整的reduced梯度
- 因此通信量为:$2\times(N-1)\times \frac{\Phi}{N} \approx 2\Phi$
效果:
- 摆脱了参数服务器的编程框架,各个Worker地位相同,解决了参数服务器方式中通讯负载不均的问题
- 每次iteration,单卡总通讯量为$2\times(N-1)\times \frac{\Phi}{N} \approx 2\Phi$,系统总通讯量为$2\times(N-1)\times \frac{\Phi}{N} \times N \approx 2N\Phi$。DDP与DP通讯量相同,但是DDP通讯负载均衡
实现细节:梯度分桶(Gradient Bucketing)
原理:(不局限于大模型)
论文中的原话是:instead of launching a dedicated AllReduce immediately when each gradient tensor becomes available, DDP can achieve higher throughput and lower latency if it waits for a short period of time and buckets multiple gradients into one AllReduce operation. This would be especially helpful for models with many small parameters. However, DDP should not communicate all gradients in one single AllReduce, otherwise, no communication can start before the computation is over.
集合通信在小tensor上性能较差,在大tensor上性能较好,因此尽可能将模型的梯度lazy allreduce,将多个小梯度打包然后再allreduce。下图中表示对于一个60M的fp32 torc.Tensor,横轴是将该tensor切成不同大小的tensor进行allreduce,纵轴表示通信时间。

对于一个大梯度,也不要只使用一个allreduce来通信。这主要考虑到计算和通信的overlap,将梯度的计算和梯度的allreduce通信进行重叠
所以梯度分桶的做法将模型的Model的参数逆序插入每个Bucket中,当一个Bucket的参数的梯度都已经更新时,开启Allreduce,向另一个节点的对应Bucket传递梯度,这样也同时实现了异步AllReduce。更详细的过程可以阅读这篇博客:Pytorch Distributed Data Parallal
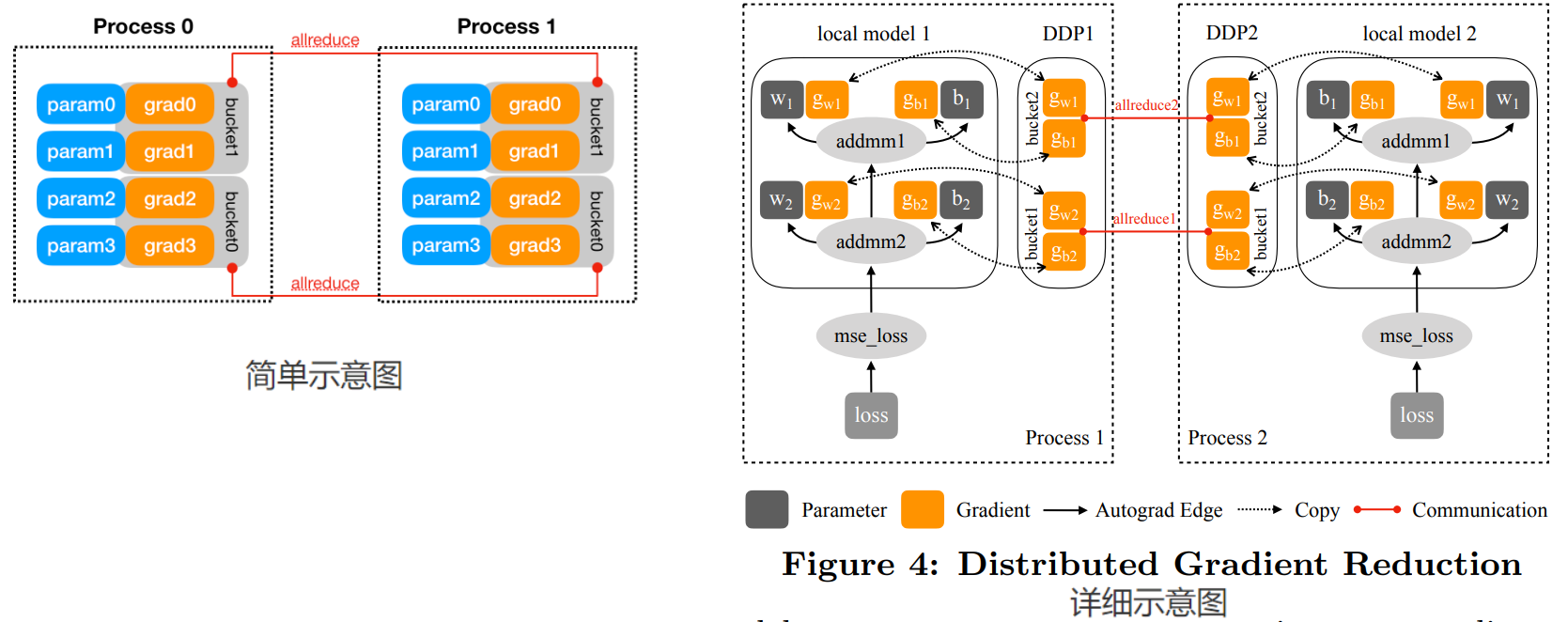
参考:
ZeRO内存优化
背景:DP或DDP中,每个GPU中都有一份完整的模型,模型变大后,不仅仅是模型参数量更占显存了,同时训练过程中的优化器状态、梯度等也相应变大了,而显存是有限的,因此要尽可能节省显存。ZeRO就是对优化器状态、梯度这部分显存的优化。
核心思想:通信换空间。优化器状态、优化器中混合精度训练时使用的fp32参数 在前向、反向时不使用,只有在参数更新时才使用,即计算过程中内存出现了冗余。因此将这些内容放在放在不同的GPU上,使用时再经过通讯获取到完成的一份。
关于模型在训练时,显存中到底存了哪些东西,可以参考GPU上都存了哪些东西;混合精度训练,可以参考混合精度训练
具体方法:ZeRO-DP、ZeRO-R,ZeRO-Offload是三种正交的显存优化方法
ZeRO-DP:是针对model states的优化,ZeRO-1、ZeRO-2、ZeRO-3是三种不同程度的优化
ZeRO-1($P_{os}$):将optimizer states和fp32参数切分,每次迭代中,
将batch分成N个mini-batch,每个GPU输入一个mini-batch,每个GPU有一份完整的fp16的参数,经过前向反向,可以得到一份完整的un-reduced梯度
每个GPU上的完整的un-reduced梯度进行一次All-Reduce,每个GPU上都得到了一份完整的reduced梯度,单卡通信$2\times(N-1)\times \frac{\Phi}{N} \approx 2\Phi$
每个GPU上只有一块不完整的optimizer states,因此只能更新对应的一块不完整的参数
每个GPU上不完整的参数进行一次All-Gather,此时每个GPU上都得到了一次迭代后、更新后的完整的参数,单卡通信$(N-1)\times \frac{\Phi}{N} \approx \Phi$
但是上述方法不是最优的(单卡通信量为$3\Phi$),更优的方法(单卡通信量为$2\Phi$)为:
- 将batch分成N个mini-batch,每个GPU输入一个mini-batch,每个GPU有一份完整的fp16的参数,因此可以得到一份完整的un-reduced梯度(同上)
- 每个GPU上的完整的un-reduced梯度进行一次Reduce-Scatter,每个GPU上都有一块不完整的reduced梯度,单卡通信$(N-1)\times \frac{\Phi}{N} \approx \Phi$
- 每个GPU上有且只有对应的一块不完整的optimizer states,因此正好更新一块不完整的参数,得到updated参数
- 每个GPU上不完整的updated参数进行一次All-Gather,此时每个GPU上都得到了一次迭代后、更新后的完整的参数,单卡通信$(N-1)\times \frac{\Phi}{N} \approx \Phi$
ZeRO-2($P_{os}+P_g$):将optimizer state和fp32参数、梯度切分,(过程同上面那种更优的方法)
- 将batch分成N个mini-batch,每个GPU输入一个mini-batch,每个GPU有一份完整的fp16的参数,因此可以得到一份完整的un-reduced梯度
- 每个GPU上的完整的un-reduced梯度进行一次Reduce-Scatter,每个GPU上都有一块不完整的reduced梯度,单卡通信$(N-1)\times \frac{\Phi}{N} \approx \Phi$
- 每个GPU上有且只有对应的一块不完整的optimizer states,因此正好更新一块不完整的参数,得到updated参数
- 每个GPU上不完整的updated参数进行一次All-Gather,此时每个GPU上都得到了一次迭代后、更新后的完整的参数,单卡通信$(N-1)\times \frac{\Phi}{N} \approx \Phi$
ZeRO-3($P_{os} + P_g + P_p$):将optimizer state和fp32参数、梯度、fp16参数切分
- 将batch分成N个mini-batch,每个GPU输入一个mini-batch,此时每个GPU只有一份不完整的fp16参数
- forward过程中,对不完整的fp16参数进行一次All-Gather,每个GPU得到了一份完整的fp16参数,可以进行forward。forward完成后,丢弃掉刚才All-Gather得到的fp16参数。单卡通信$(N-1)\times \frac{\Phi}{N} \approx \Phi$
- backward过程中,再次同样对不完整的fp16参数进行一次All-Gather,每个GPU得到了一份完整的fp16参数,可以进行backward,得到一份完整的un-reduced梯度,单卡通信$(N-1)\times \frac{\Phi}{N} \approx \Phi$
- 每个GPU上的完整的un-reduced梯度进行一次Reduce-Scatter,每个GPU上都有一块不完整的reduced梯度,并且丢弃掉剩余的梯度,单卡通信$(N-1)\times \frac{\Phi}{N} \approx \Phi$
- 此时每个GPU上有一块不完整的optmizer states和一块不完整的reduced梯度,正好更新对应的一块不完整的参数,得到一块不完整的updated参数,而且此时不需要对不完整的update参数进行All-Gather操作(因为本来就是被切开的)
- 将batch分成N个mini-batch,每个GPU输入一个mini-batch,此时每个GPU只有一份不完整的fp16参数
ZeRO-R:针对residual state的优化
- $P_a$:针对中间激活值,激活值只起到一个加速计算梯度的作用,这里将激活值也进行切分,每个GPU上保存一份,在反向计算梯度需要完整的激活值时再经过通讯获取完整的激活值
- $C_B$:针对一些操作或算子需要开辟buffer或者临时数组,这里预先开辟较大的内存buffer,并在后续保持固定
- $M_D$:针对频繁内存申请和释放可能导致的内存碎片,这里将内存大致分为两个部分,long lived参数放在一个部分,将另一些经常构造析构的中间激活值等放在另一个部分
ZeRO-Offload:
- forward和backward计算量大,因此将fp16的参数、激活值放在显存中
- 更新参数的计算量小,因此将optimizer state(和fp32参数)、梯度放在内存中
效果:
- 通信方面:ZeRO-1和ZeRO-2相较于DP或者DDP没有增加通信量,ZeRO-3仅仅增加了0.5倍的通信量。
- 显存方面:极大降低了(单卡)显存占用。图中K=12,是对应fp32 param(4)+fp32 momentum(4)+fp32 variance(4);前面两个2分别是fp16 param(2)和fp16 grad(2)
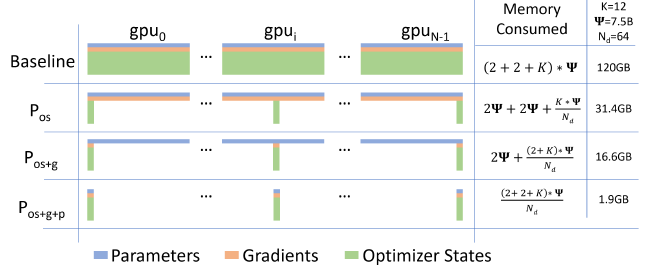
其他说明:
- 为什么ZeRO是数据并行?明明把优化器状态、梯度甚至参数切开了
- 模型并行是只使用自己那部分参数进行计算,将中间结果(激活值)进行通讯(比如TP)
- ZeRO-DP将优化器状态、参数、梯度等切分放到多个GPU上,ZeRO-R将输入和中间激活值切分开放到多个GPU上,在实际运算时,每张卡上输入的mini-batch不相同,首先需要经过通讯,拿来完整的输入和完整的参数进行前向计算,拿来完整的中间激活和完整的权重反向传播计算梯度,因此ZeRO只是内存优化后的数据并行
参考:
- 图解大模型训练之:数据并行下篇( DeepSpeed ZeRO,零冗余优化)
- ZeRO: Zero Redundancy Optimizer,一篇就够了
- 分布式训练:了解Deepspeed中的ZeRO1/2/3
FSDP(FullyShardedDataParallel)
FSDP是DeepSpeed ZeRO-DP的进一步发展,主要实现了与PyTorch的co-design,改进主要体现在计算和通信的粒度,FSDP中前反向的计算都是以FSDP unit为粒度执行的。
(need further understanding)
推荐好文:
流水线并行
流水线并行大致可以这样进行分类:
- 同步流水线
- F-then-B:GPipe
- 1F1B
- non-itlv:PipeDream-flush
- itlv:
- parallel-shape:Megatron-2
- v-shape:Zero-Bubble-V
- 1F2B:Zero-Bubble
- 异步流水线:
- PipeDream
- PipeDream-2BW
使用流水线并行有两点需要注意:
流水线并行的通信量不大,因为只涉及到不同stage输入的通信(后面一维张量并行中会比较PP、DP、TP的通信量)。这里符号沿用LLM时代的transformer参数量、计算量、激活值的分析,并设置一些新的符号表示:设micro-batch数量为m,每个micro-batch的大小为$b_m$(因此有$m \times b_m = b$,将模型划分为$N_s+1$个stage(或者叫做cell,chunk,在interleave场景下是virutal stage的数量),流水并行度即文章开头提到的$p$。(下面以transformer为例进行分析)
一个micro-batch在一个stage的通信量是$w \times 2\times b_m sh$(2表示FWD过程中要将输出激活值通信+BWD过程中要将对输入激活值的梯度进行通信),m个micro-batch在切分成$N_s+1$个stage时,总的需要通信的数据大小为$m \times 2wb_msh \times N_s=2wbshN_s$,每个Device的通信量为$\frac{2wbshN_s}{p}$
我们来举几个例子,来量化感受一下(假设使用缓和精度训练,w=2,1F1B,non-itlv)
model b s h 单层单次通信量$wbsh$ GPT-3 175B 1 2048 12288 96MB Llama-2 70B 1 2048 8192 128MB Llama-3 405B 1 4096 12288 192MB
PP不推荐ZeRO-2/ZeRO-3同时使用,原因在于增加了很多通信,但是缺节省不了多少下显存。
下图中是PP+ZeRO-2的示意图,dp_size = 2,每个DP内部又划分为p = 4的PP。每个DP吃掉的mini-batch都是不同的,PP又将每个DP吃掉的mini-batch再次切分为micro-batch,即图中DP1对应micro-batch1~4,DP2对应micro-batch5~8。注意,由于使用ZeRO-2(或ZeRO-3),会对反向得到的梯度进行切分,DP1反向得到完整的un-reduced梯度,DP2反向得到完整的un-reduced梯度,然后进行Reduce-Scatter通信(比如GPU4上mbs1的梯度要与GPU8上mbs5的梯度进行Reduce-Scatter通信),DP1得到不完整的reduced梯度(即前半部分参数对应的梯度),DP2得到不完整的reduced梯度(即后半部分参数对应的梯度)。除此之外,由于PP使用梯度累计,所以最后UPD先进行梯度累积,然后使用不完整的redued梯度更新完权重后,还要进行All-Gather通信拿到完整的权重(因为ZeRO-2没有切权重)。如果是PP+ZeRO-3,则要在每个mbs的前向过程之前进行一次All-Gather,在mbs的反向过程之前进行一次All-Gather,反向过程之后进行一次Reduce-Scatter,最后的All-Gather可以省去。

针对大模型而言,PP一般是要使用的,此时再使用ZeRO就是想减少单卡的内存占用。一方面,我们来看一下PP+ZeRO-2对减少内存占用的一个效果,PP切分模型后,每个stage上的参数量基本上是整个模型参数量的$\frac{1}{N_s+1}$,ZeRO-2又切分了梯度,相比于ZeRO-1内存占用减少了$\frac{1}{N_s+1}(1-\frac{1}{N})w\Phi$(如果进一步使用TP并行进行切分,则会进一步减小内存占用,这个内存减少的量也会进一步减小),因此,使用PP后再使用ZeRO-2可能节省不了多少显存。另一方面,从通信量来分析,由于ZeRO-2的梯度切分,反向得到梯度后要在DP group间通信,PP将mini-batch切分为micro-batch,又使得梯度Reduce-Scatter变得很频繁(相当于DP group变多),每一次Reduce-Scatter通信量都是两倍的对应梯度大小再乘以数值精度,通信量直接暴涨(虽然有可能做到计算和通信overlap,我也不太确定这一点,但是毕竟性能肯定还是有损失的)。PP+ZeRO-3也是同理,显存占用可能再少一点,但是带来的通信量增加是很大的。因此,在PP基础上使用ZeRO-2(或者ZeRO-3)节省不了多少显存,还会增加很多通信量,对性能的提升可能很有限甚至负提升。可以参考知乎问题:大模型训练时ZeRO-2、ZeRO-3能否和Pipeline并行相结合?
但是可以PP+ZeRO-1(比如下图),由于梯度(和权重)都是完整的,先进行完整的un-reduced梯度的梯度累积,然后进行Reduce-Scatter通信,得到不完整的reduced梯度,ZeRO-1只会切分optimizer_states(和混合精度中使用到的fp32权重),正好更新那一部分权重,最后使用All-Gather通信拿到全部的权重。

参考:
naive流水线并行:F-then-B
如果模型太大(参数量太大),单卡装不下时,将模型横着切,每个部分(可能是多层,称为一个chunk)放在一个GPU上:
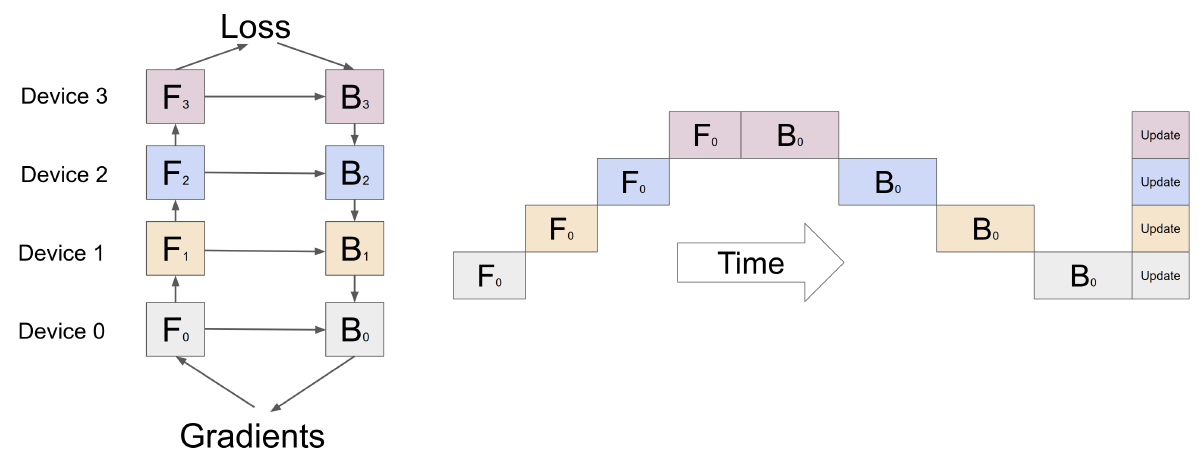
模型可以训练起来,但是一个缺点,就是GPU利用率不高,bubble很多,某一时刻只有一个GPU在进行计算。
GPipe:micro-batch
GPipe主要是针对naive流水线并行的改进,主要是提升GPU利用率,减少bubble占比。
具体方法是,同样将模型横切,划分为多个cell(每个cell包含若干个连续的层,原来叫做chunk,后面PipeDream又叫做stage,一个意思),每个cell放在一块GPU上。将输入mini-batch再划分为micro-batch,将多个micro-batch依次送入到模型中,形成流水线,这种策略也叫F-then-B。简单来说,模型切法没变,batch切开。
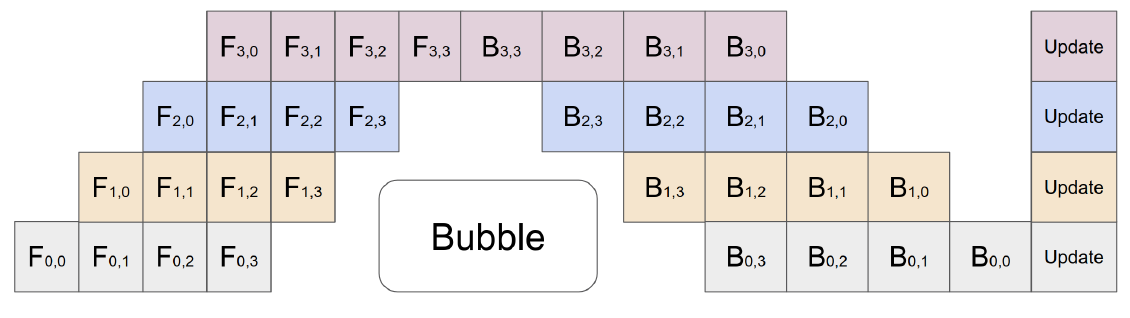
第一个下标表示GPU编号(或者cell编号),第二个下标表示micro-batch编号,横轴表示时间,纵轴表示不同GPU。比如$F_{0,1}$ 表示第1个micro-batch作为cell0(对应GPU0)的输入。假设划分为M个micro-batch,则bubble占比为$\frac{N-1}{M+N-1}$。
有一个细节需要注意,将mini-batch切成micro-batch,会对Batch norm的计算有影响,因为原来BN是对整个batch的相同channel进行norm,现在整个batch被拆开成好几个micro-batch,每个micro-batch都能单独计算一个BN,但是同时还维护一个全局的、针对所有micro-batch的移动平均和方差,以供最后推理阶段使用。但是LLM或者NLP中使用BN好像不多,且micro-batch对LN没有影响(本来LN就是对每个token内部算均值方差)。
GPipe论文中还提出了一个优化显存的方法:重计算(re-materialization,或者re-compute,也叫做active checkpoint,activation checkpoint),重计算不属于流水线并行(也不属于各种并行),这里简单介绍一下。在反向传播计算梯度的时候,需要上一层传来的梯度、该层的参数,还可能需要该层的输入激活值,如果在前向过程中这个激活值没有保留的话,就需要从之前的某个起点开始重新走一遍前向过程得到这个激活值,流水线并行恰巧比较方便确定这个起点,就是每个cell的输入。重计算降低的是峰值显存。
GPipe有两个缺点:
只有将模型划分得比较均匀时,流水线并行才能得到较为理想的效果;但是有的模型不太好均匀划分
每个GPU,需要缓存每个micro-batch前向过程中的输入和所有的中间激活,一个解决方法是开重计算,开重计算后,每个GPU只需要缓存每个cell的输入即可,属于是时间换空间了。
- 为了降低空泡比,就要增大micro-batch的数量,假设原来mini-batch大小不变,中间激活大小也没变,但是每个micro-batch大小就变小了,太小会导致计算效率变低。可以参考大模型效率工程(五):一文读懂流水线并行训练升级之路 —— From Naive to V-shape Zero Bubble中3.2节
但是也会增加峰值显存。
参考:
PipeDream:1F1B
PipeDream是一种异步流水线的方案,同时维护多个版本的权重,每次反向传播都会更新权重,PipeDream论文中提到的weight Stashing和vertical Sync(论文中说vertical Sync可以忽略),个人理解不是很透彻(水平方向上可以使用weight stash保证每个micro-batch更新的是对应版本的权重,但是竖直方向上Device4每次都更新权重,Device1上将梯度更新平均到了4个版本的weight上,最后训练出来,权重到底怎么算?),这里先暂且略过,待后续更新。
PipeDream论文中提出了1F1B流水线并行策略,但它是异步的;Memory-Efficient Pipeline-Parallel DNN Training中提出了PipeDream-Flush(这是同步版本的1F1B流水线)和PipeDream-2BW(这也是异步版本的1F1B流水线,但它减少了对weight stash的维护)
这里主要来描述一下同步流水线1F1B流水线并行策略,一个micro-batch的前向计算可以和另一个micro-batch的反向计算交叉进行,从而可以及时释放不必要的中间激活。因为是同步的,所以此时没有了weight stash。图中标号表示不同的micro-batch;蓝色块表示前向过程,每个同步阶段、每个stage都是基于相同的参数、吃掉不同的micro-batch;绿色块表示反向过程,每个stage基于相同的参数、使用与对应前向过程的中间激活(比如GPU0上吃掉micro-batch0,前向和反向中间有间隔,需要保证对应),得到梯度(实际上应该是累计的梯度);红色块表示使用梯度更新参数。
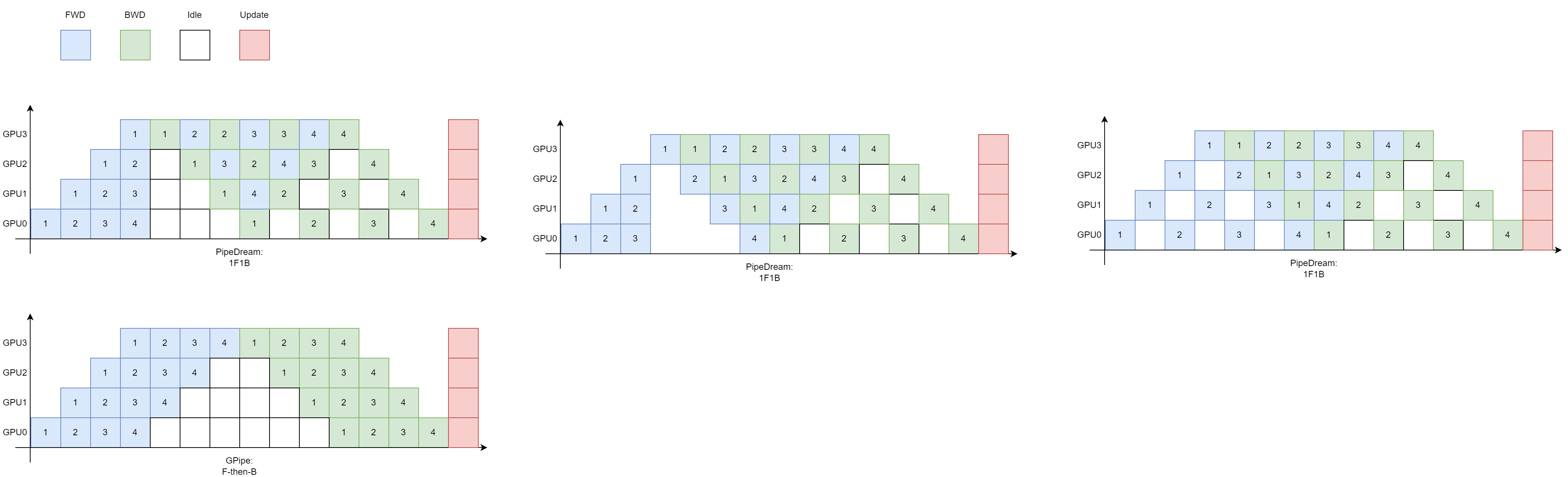
第一行三个图实际上是相同的,区别只是在于一开始前面几个micro-batch输入顺序有稍许不同(只要能保证上下游的依赖关系,可以随便调整)。这幅图除了示意说明1F1B,还说明了1F1B与F-then-B的耗时是相同的,bubble也是相同的。1F1B相较于F-then-B的优点,在于减少了中间激活,节省显存。GPipe前向过程中需要将每个micro-batch计算的中间激活值保留下来,而在1F1B中,分别需要保存4、3、2、1份中间激活,stage0中需要保存micro-batch 1~4计算的中间激活值,stage1中需要保存micro-batch 1~3计算的中间激活值,stage2中需要保存micro-batch 1~2计算的中间激活值,stage3中只需要保存一份micro-batch计算的中间激活值,因为随后的对应的反向计算中会使用该中间激活,使用完可以丢弃(或者由于LLM的规整性,可以复用),以后不会用到这些中间激活了。节省显存之后,就可以使用更多的micro-batch数量,从而达到减少bubble的目的。
有一点需要注意,GPipe中,增大micro-batch数量不会降低显存占用,但是在1F1B中是可以的,更准确来说是,增大micro-batch数量,Device1的峰值显存在1F1B中会更少,相较于GPipe。比如原来micro-batch数量是4,现在micro-batch增大到8,那么GPipe中还是F-then-B的方法,但是1F1B中可以调整流水线编排:(上面GPipe的图中省略了micro-batch的标号,下面1F1B的编排中Device1最多只有4份中间激活)
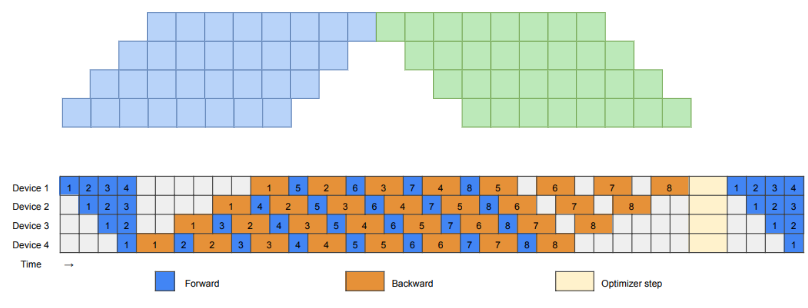
针对PipeDream和GPipe,而且也属于是1F1B的一个改进是PipeDream-2BW,可以看作是PipeDream和GPipe的折中和结合,PipeDream的异步+Gpipe的梯度累计更新参数+double-buffer。具体而言,就是流水线总体上是异步的没有flush(类似PipeDream),但是现在只维护了两个weight buffer;每输入m个micro-batch使用相同的权重,然后进行一次梯度累计和梯度更新(类似于GPipe,不像PipeDream是每输入一个micro-batch都要梯度更新);对权重使用double-buffer,每隔m个micro-batch,更新旧的weight,后面接着的m个micro-batch切换weight。
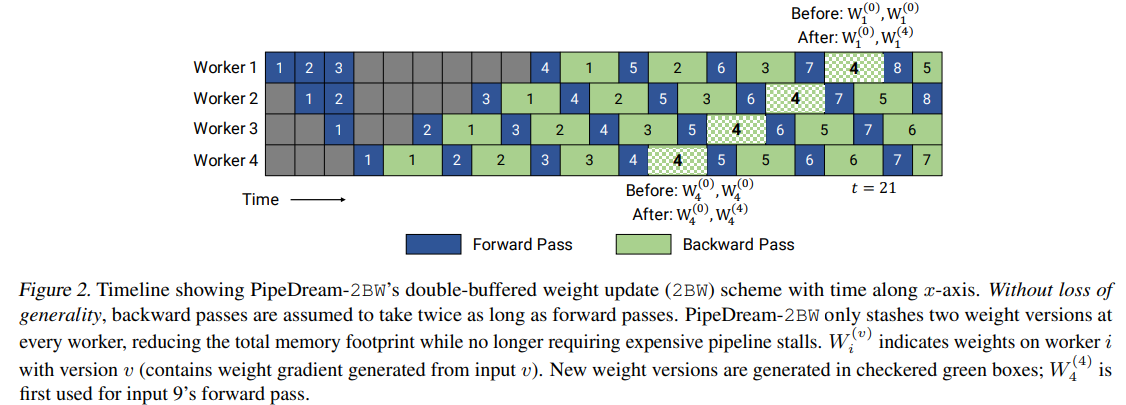
Megatron-2:interleave(itlv)
将模型分为多个chuck(若干个连续的层构成一个chuck,或者叫做virtual stage),每张卡上放2个以上的chuck,比如下面图示中,比如Device1上有两个chunk(0、1层组成一个chunk,8、9层组成一个chunk),micro-batch1分别经过device1的chunk1(0,1层)、device2的chunk1(2,3层)、device3的chunk1(4,5层)、device4的chunk1(6,7层)后,再返回,经过device1的chunk2(8,9层)、device2的chunk2(10,11层)、device3的chunk2(12,13层)、device4的chunk2(14,15层)。深色表示该Device上的第一个chunk,浅色表示第二个chunk。
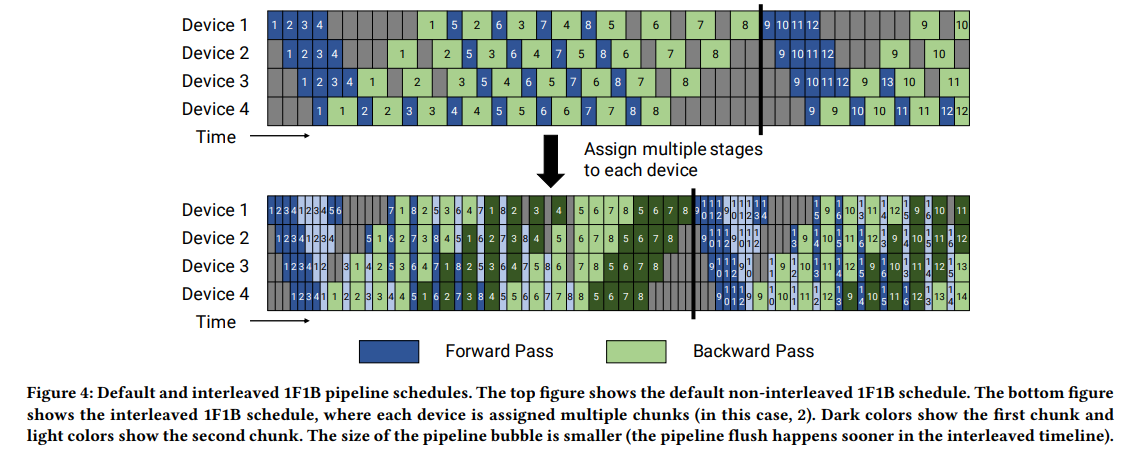
该方案要求micro-batch数量是Device数量的整数倍,因此才能最大程度的减少bubble。假设原来一个stage切成了v个virtual stage(或者chunk),一个mini-batch切成了m个micro-batch,气泡占比从原来的$\frac{(p-1)(Time_{FWD}+Time_{BWD})}{m(Time_{FWD}+Time_{BWD})}=\frac{p-1}{m}$降低到$\frac{(p-1)(Time_{FWD} / v+Time_{BWD} / v)}{m (Time_{FWD}+Time_{BWD})}=\frac{1}{v} \times \frac{p-1}{m}$,但是代价是PP之间的通信也变为原来的v倍。
Zero-Bubble:1F2B
原来流水线基本都是FWD和BWD相重叠,Zeor-Bubble中将BWD的过程进一步细化,进行拆分:
反向过程中要计算对权重的梯度,这个过程记为W
反向过程中要计算对输入的梯度,这个过程记为B
一般来说,参数梯度计算耗时W < 前向过程计算耗时F < 激活值梯度计算耗时B
原来B过程和W过程都融合在一起,只有二者都完成,才能进行下一个stage的反向。但是中间存在一个不必要的依赖:第i-1层的B过程隐式的依赖于第i层的W过程,或者说,原来只有$B_i$和$W_i$都完成了,才能进行$B_{i-1}$和$W_{i-1}$的过程,而实际上,只要$B_i$完成了,就能进行$B_{i-1}$和$W_{i-1}$的过程。甚至最极端的情况是,先完成所有的B过程,然后再进行W过程,来更新参数。
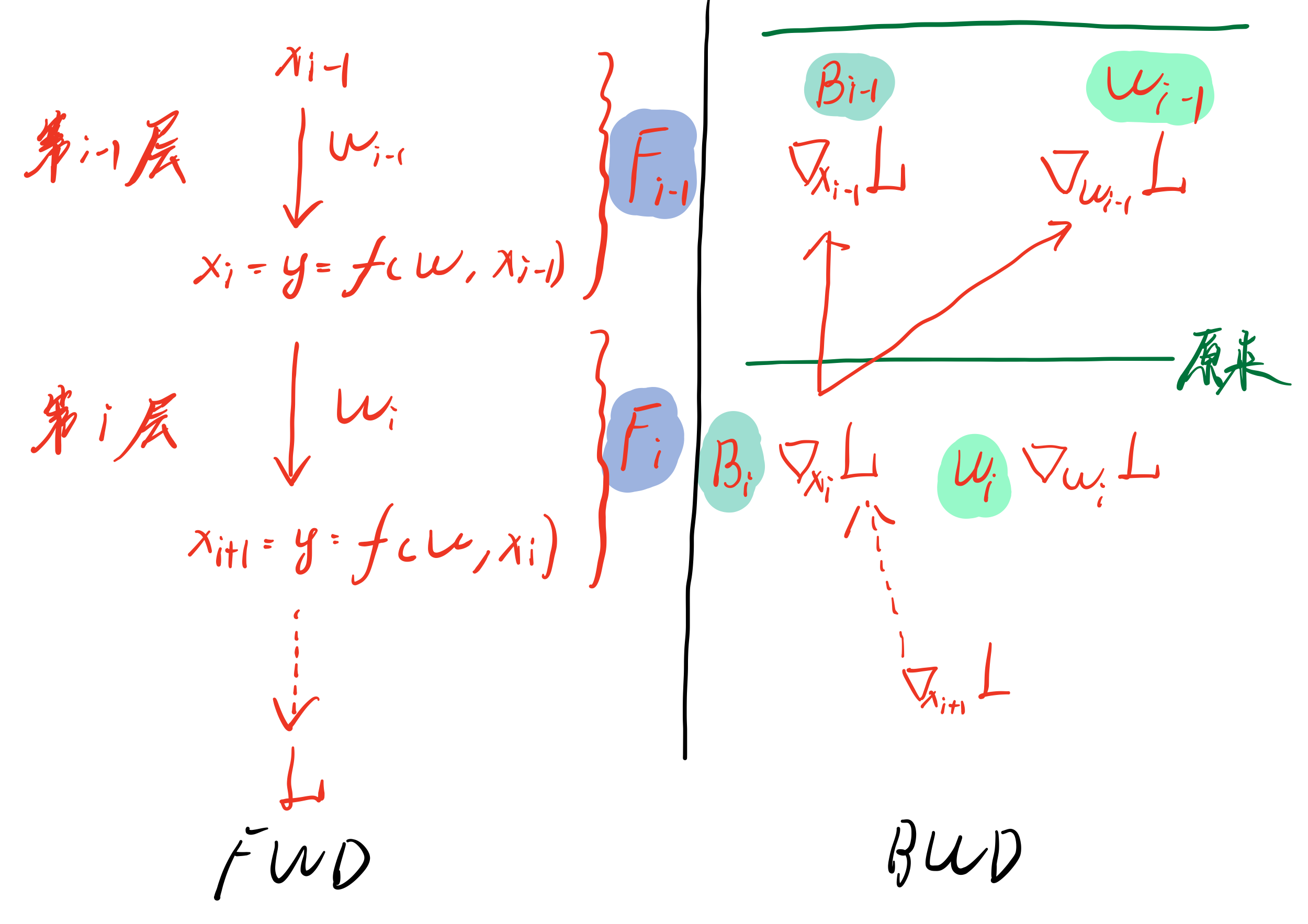
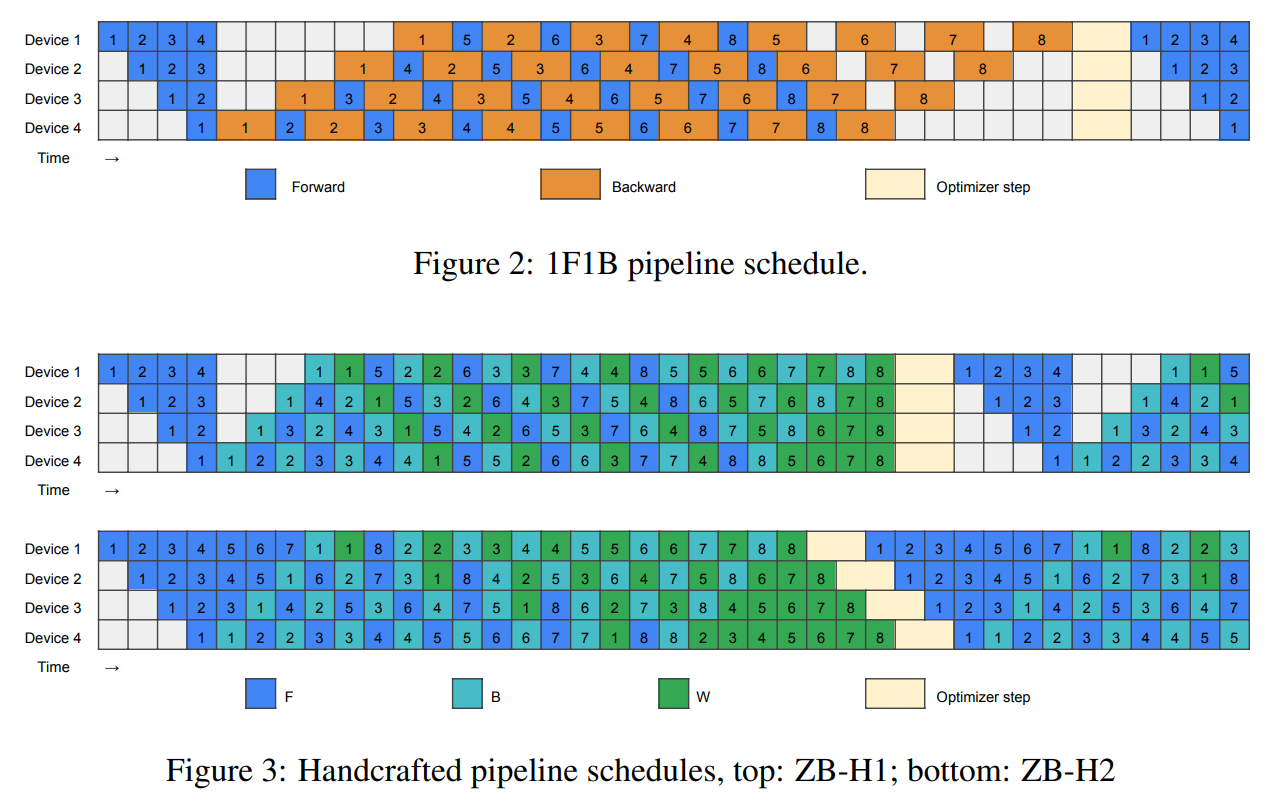
来自相同micro-batch的F过程和B过程仍然要保持先F后B的dependency,W过程只要保证在上一个micro-batch的B过程之后就可以,比较灵活,因此可以进行手工调整以减少气泡,这是两个手工设计的流水线方案:
- ZB-H1:相较于1F1B,ZB-H1气泡更少,峰值显存相同,主要是因为B过程提前,而且尾部的气泡可以被W填充
- B过程和W过程计算时需要的激活值的显存分别记为$M_B=bs(34h+5as)$和$M_W=32bsh$,第i个Device:
- ZB-H1占用显存$(p-i+1)M_B+(i-1)M_W$,其他Device的显存占用不会比Device1显存少太多
- 1F1B占用显存$(p-i+1)M_B$,其他Device的显存占用明显少于Device1
- B过程和W过程计算时需要的激活值的显存分别记为$M_B=bs(34h+5as)$和$M_W=32bsh$,第i个Device:
- ZB-H2:ZB-H2的气泡更少,但是峰值显存会变多
- 第i个Device,ZB-H2占用显存$(2p-2i+1)M_B+2(i-1)M_W$,相比于ZB-H1显存几乎翻倍
- 论文中附录F中说到,用显存换ZB-H2是值得的,在相同显存的情况下,ZB-H2的micro-batch size可以是1F1B的一半,由于大模型训练中几乎不存在设备利用率不饱和的情况,所以减小micro-batch size,以换取更少的bubble,这么看是值得的,况且显存可以使用ZeRO等方式进行优化。
参考:
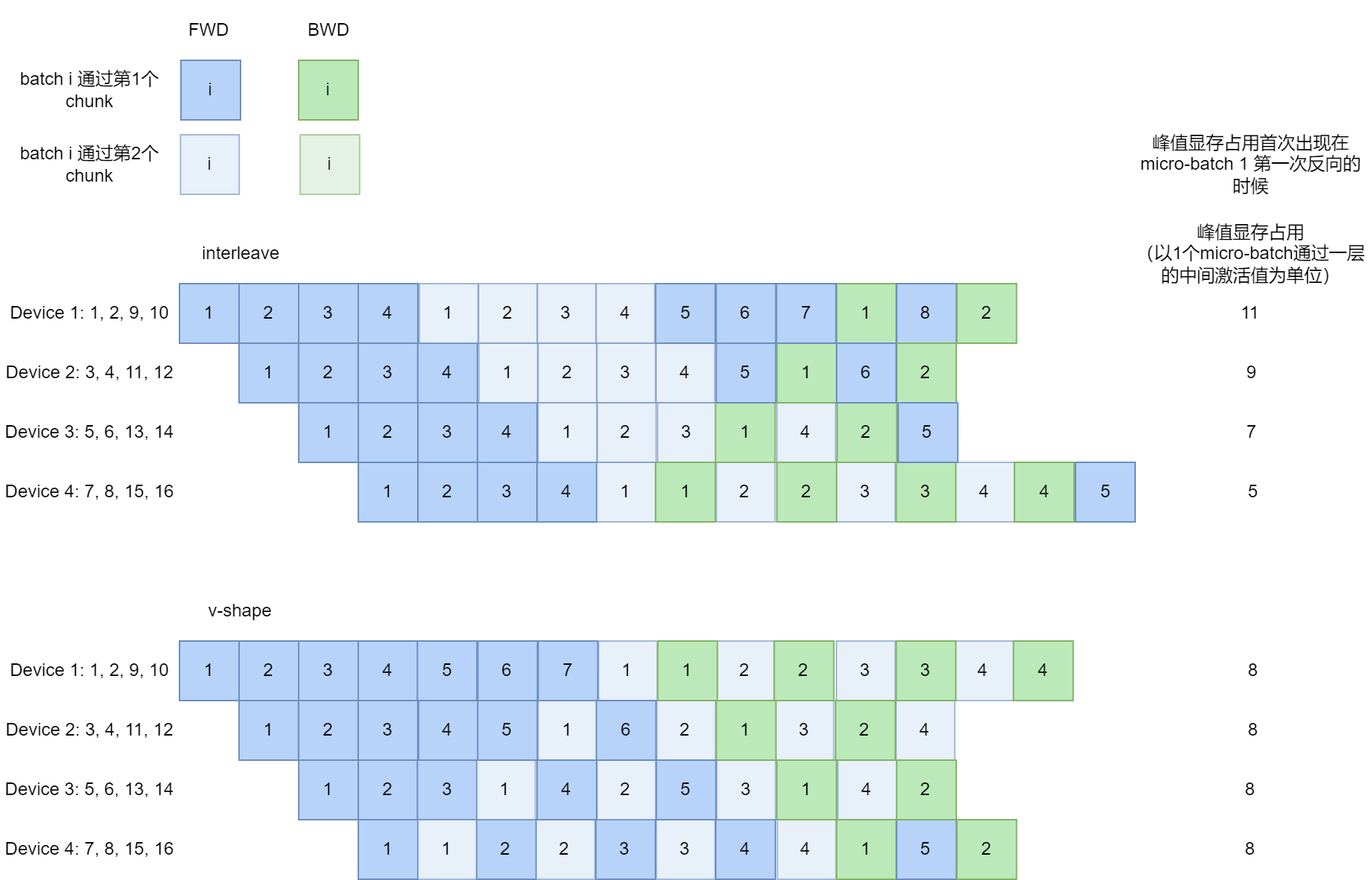
V-shape
首先说明,V-shape是在1F1B itlv的情况下的一个流水线模式。1F1B itlv(vpp)是左边的模式,第二次通过流水线的时候是顺序的,比如3个Device,模型6层(分成6个chunk,每层两个chunk),Device1上放1、4层,Device2上放2、5层,Device3上放3,6层。V-shape中,第二次通过流水线是倒序的,Device1上放1、6层,Device2上放2、5层,Device3上放3,4层。
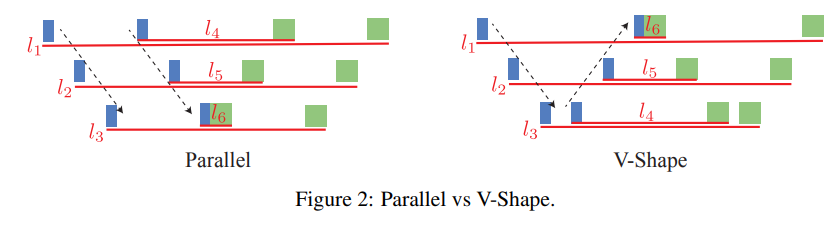
Zero Bubble Pipeline Parallelism (Arxiv版本)在第6节介绍了 V-shape Zero Bubble Pipeline Parallelism,名为ZB-V,Pipeline Parallelism with Controllable Memory 对 V-shape 进行了系统性介绍,称 V-shape Zero Bubble PP 为 V-ZB。V-shape最主要的作用就是减少峰值显存,峰值显存降低到与1F1B相同(V-shape和Parallel-shape的通信还是相同的),下面是对比:
Hanayo
【分布式训练技术分享九】聊聊高效流水并行Hanayo: Harnessing Wave-like Pipeline Parallelism
张量并行
流水线并行是将模型按层横着切分,张量并行是将模型按列切分,每张卡上放一块不完整的权重,以减少内存占用。
首先来看如何对$Y=XW$的矩阵乘法进行TP切分,这是模型张量并行的基础。
RowParallel:对W按行切分,此时X要按列切分,比如切成两份,X1、W1、Y1放在GPU1上,X2、W2、Y2放在GPU2上,Y在每个GPU上都有一份
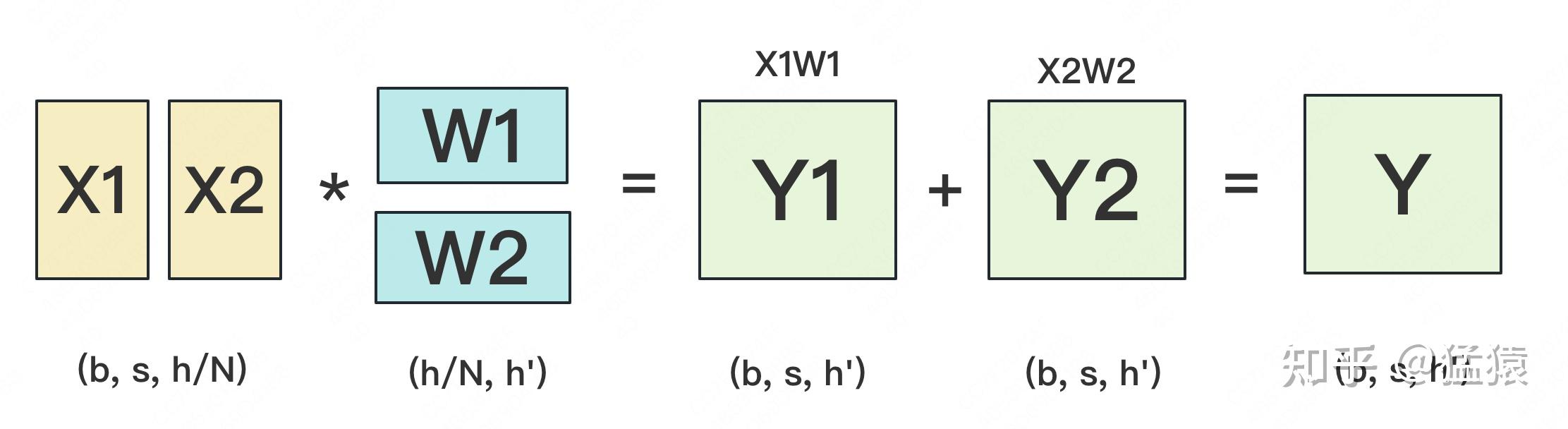
深度学习中,不仅要有Y=XW的前向计算,还要进行反向计算,求得对权重W和对输入X的梯度
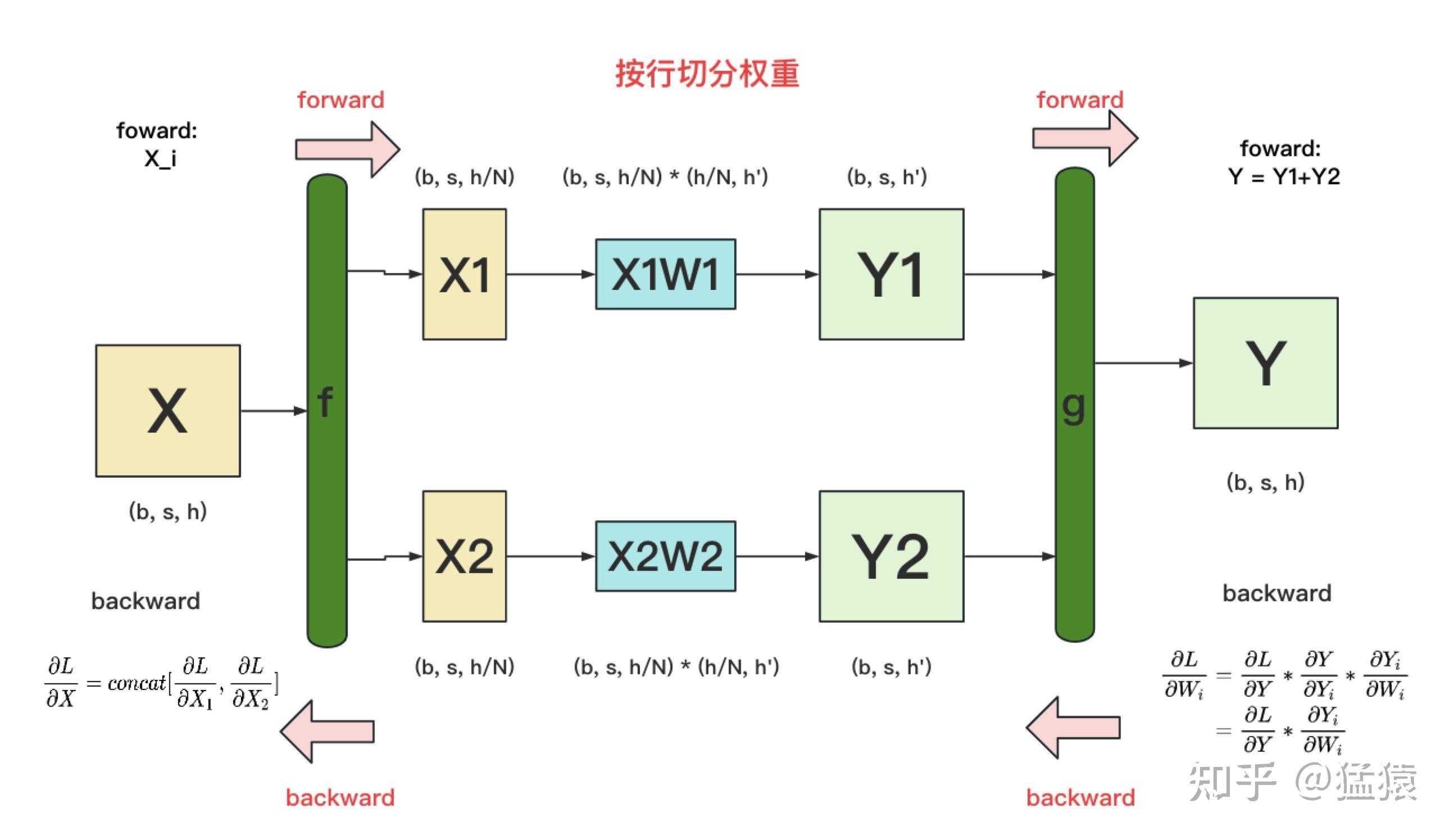
- f:
- forward:split(或者说only keep one part),原来X在每张卡上都有一份,现在GPU1上keep X1,GPU2上keep X2
- backward:all-gather,将GPU1上的X1的梯度和GPU2上X2的梯度进行all-gather通信,每张卡上都能拿到完整的X的梯度
- g:
- forward:all-reduce,将GPU1上的Y1和GPU2上的Y2进行all-reduce通信,每张卡上都有reduced的Y1+Y2
- backward:identity,或者说将Y的梯度broadcast给GPU1和GPU2
- f:
ColumParallel:对W按列切分,此时X要按行切分,比如切成两份,W1、Y1在GPU1上,W2、Y2在GPU2上,X、Y在每张卡上都有一份
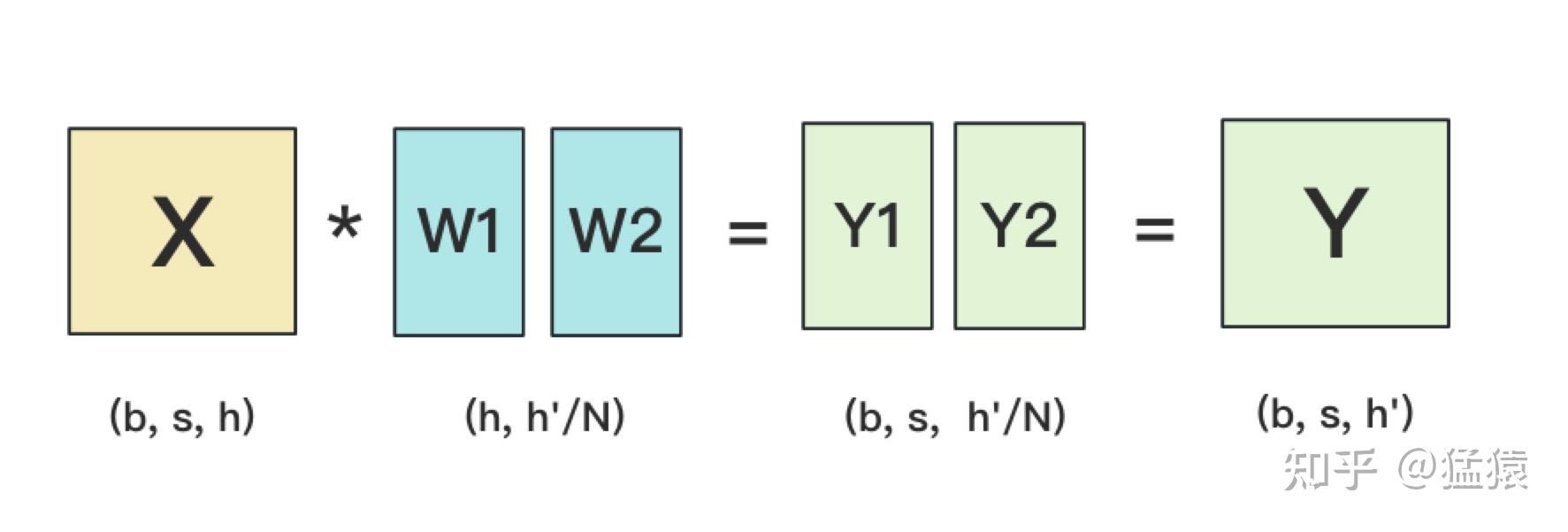
同样还要可以计算对权重W和对输入X的梯度
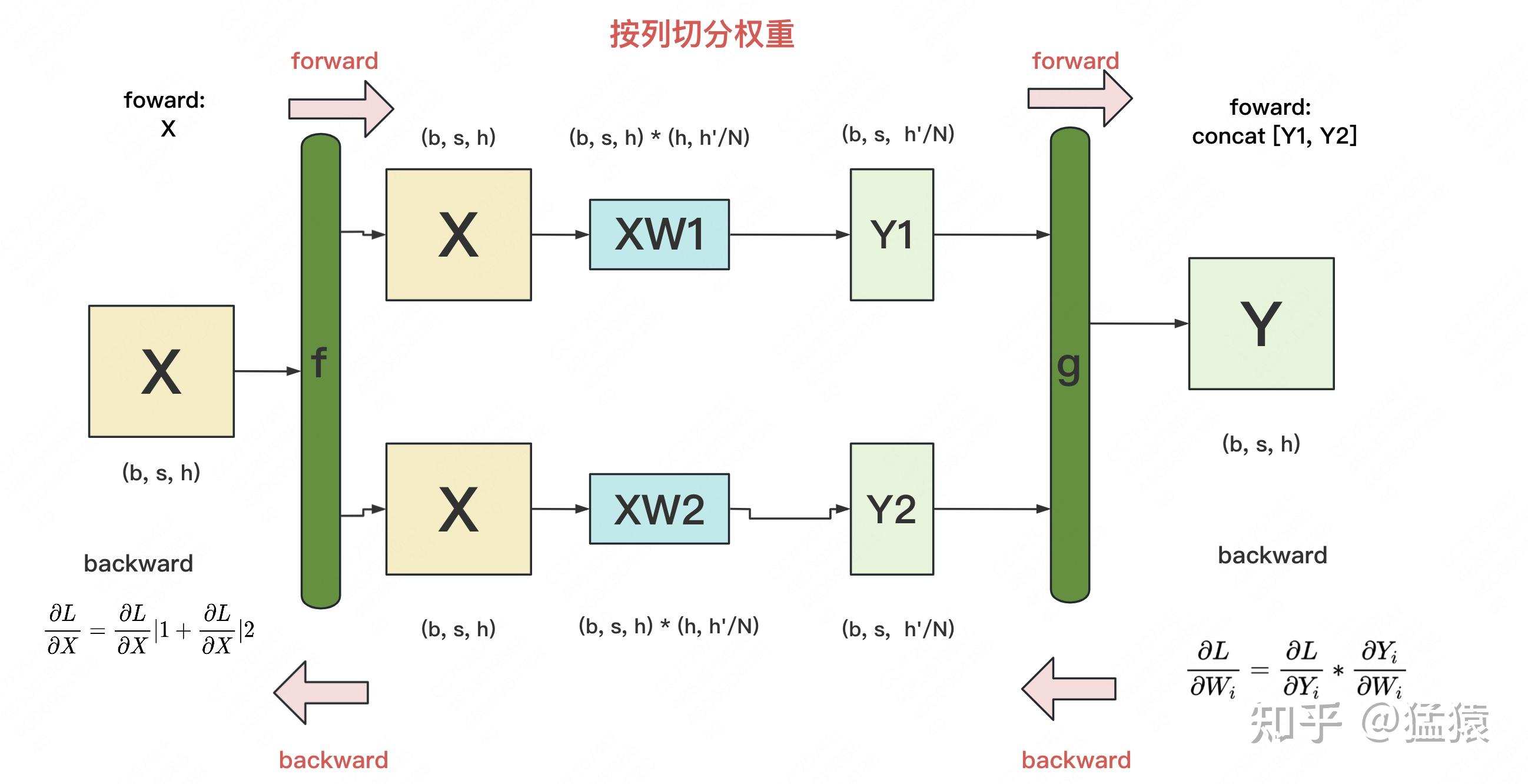
- f:
- forward:identity,或者说将X复制到每张卡上完整一份
- backward:all-reduce,将GPU1上的X的梯度和GPU2上的X的梯度进行all-reduce通信,每张卡上都有reduced的X梯度
- g:
- forward:all-gather,将GPU1上的Y1和GPU2上的Y2进行all-gather通信,每张卡上都有一份完整的Y
- backward:split(或者说only keep one part),原来Y的梯度在每张卡上都有一份,现在GPU1上keep Y1的梯度,GPU2上keep Y2的梯度
- f:
一维张量并行:Megatron-LM
具体过程
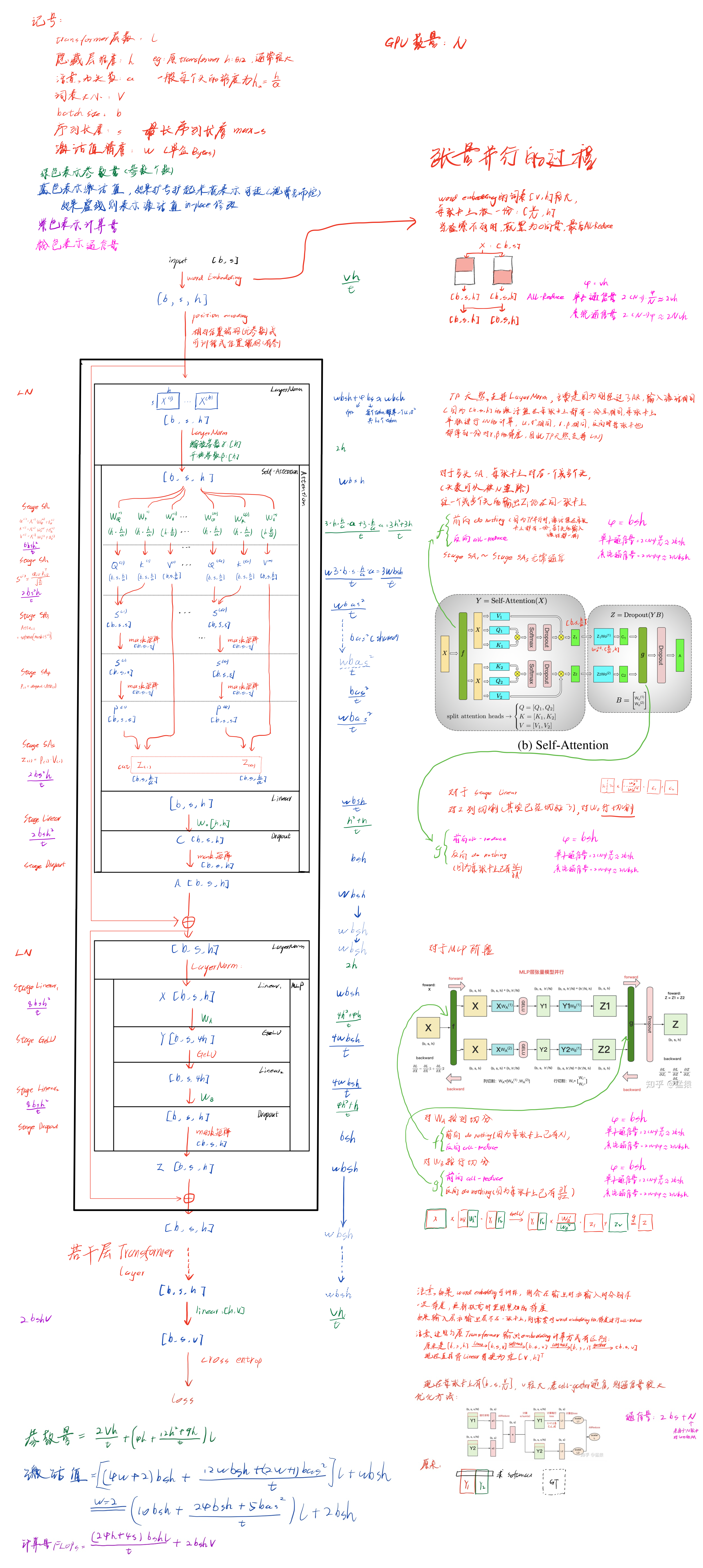
总的通信量为:$w(vh+4bsh \times l + 2bs + N)$
简要分析
DP、PP、TP通信量比较:(以整个transformer模型为例,假设w=2)
DP:输入batch,经过前向反向后得到参数的梯度,然后对梯度进行all-reduce,transformer 的参数量为$2Vh + (4h+4+3I)hl$,因此DP的通信量为:$2w\Phi = 4wVh + 2w(4h+4+3I)hl$,该通信量只与模型相关
PP:m个micro-batch(即一个mini-batch)在一个stage(一个stage可能包含多个transformer block)的通信量是$m \times 2 \times w(b_msh)=2wbsh$(non-itlv),如果整个模型切成了$N_s+1$个stage,那么通信量为$2wbshN_s$,如果是itlv(假设原来一个chunk切分为2个virtual stage)则通信量翻倍,可以看出该通信量与输入token数量、模型的隐藏层维度、模型切分的stage数量相关
TP:$w(vh+4bsh \times l + 2bs + N) \approx w(vh + 4bshl) \approx 2wbsh \times 2l$,可以看出该通信量与输入token数量、模型大小相关,而且$2l$一般大于$N_s$,所以现在就可以分析出通信量TP>PP
然后进行一个case study,来直观感受一下。因为我们在训练时总想在显存允许的范围内增大batch size、增大序列长度,一般来说TP通信量还是要比DP通信量多的(可能会有例外),但是可能没有数量级上的差距。但是TP需要频繁的进行通信,所以TP更适合在单机多卡间并行。
model h I b s $N_s$ DP通信量$\approx 4\Phi$ PP通信量$=4bshN_s$ TP通信量$\approx 8bshl$ GPT-3 175B 12288 96 8 2048 16 651.92GB 12GB 144GB Llama-2 7B(6.7B) 4096 32 8 4096 4 24.96GB 1GB 32GB Llama-2 13B 5120 40 8 4096 8 48.43GB 2.5GB 50GB Llama-2 70B 8192 80 8 4096 8 260GB 8GB 160GB Llama-3 405B 16384 126 8 4096 16 391.15GB 32GB 504GB
辨析一下TP和ZeRO-3:Github issus
- 相同点:都是将权重(和梯度)竖着切开,放在不同卡上
- 不同点:
- 输入方面:TP可以使用不完整的输入进行计算,ZeRO-3必须使用完整的输入进行计算
- 通信方面:TP通信是为了对激活值进行reduce,ZeRO-3通信是为了拿到完整的权重和梯度
- 总结就是,TP使用本地不完整的输入、本地不完整的权重进行计算,通信是为了对结果进行all-reduce;而ZeRO-3使用本地完整的输入、全局完整的权重(由通信拿来的)进行计算,通信是为了拿来全局完整的权重
- TP与ZeR-3是兼容的,但是TP+ZeRO-3(和TP+ZeRO-2)实际上就退化成了TP+ZeRO-1(TP已经切分了权重和梯度,ZeRO只是切optimizer_states和fp32权重)
效果
计算量 参数量 激活值 通信带宽 通信时延 without TP $(24h+4s)bshl+2bshV$ $2Vh+(12h^2+13h)l$ $2bsh+[34bsh+5bas^2]l$ $O(1)$ $O(1)$ with TP $\frac{(24h+4s)bshl}{t}+2bshV$ $\frac{2Vh}{t}+(4h+\frac{12h^2+9h}{t})l$ $2bsh+[10bsh+\frac{24bsh+5bas^2}{t}]l$ $O(2(t-1)t)$ $O(2(t-1))$
参考和推荐好文:
多维张量并行:Colossal-AI
个人对多维张量并行了解不深入,也没有使用过,看一些解读,感觉就像是对矩阵乘法各种拆分和在多处理器上并行,这里简单进行一下记录。
2D Tensor Parallel
背景:Megatron-LM的张量并行中,每个GPU上都要保留完整的激活,激活值没有被切分,如下图(绿色表示激活,蓝色表示权重):
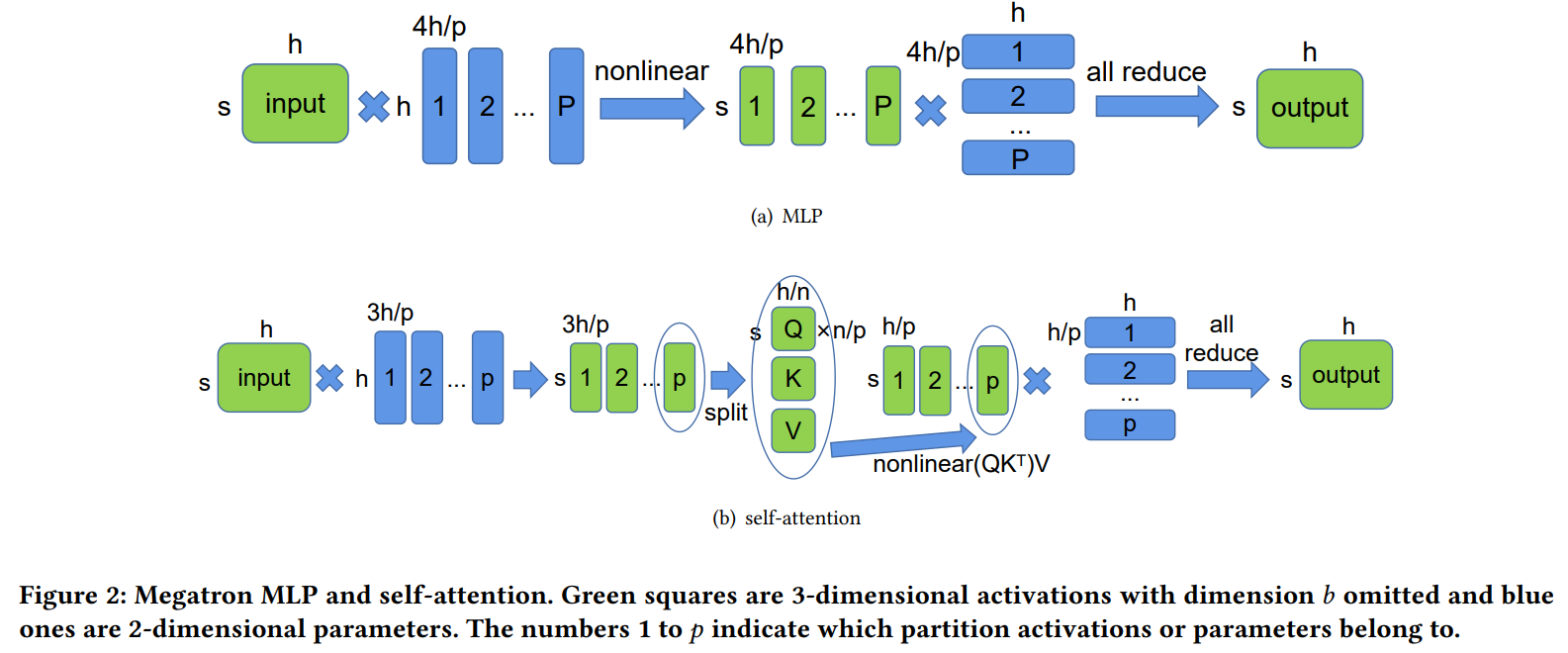
解决方法:将激活和权重划分成二维网格,一个限制是输入激活和权重需要是方阵,需要有$q\times q$个处理器,每个处理器上保留网格中的一块权重和激活值(而非完整的激活值),因为Transformer中很多都是矩阵乘,所以中间可以使用SUMMA并行矩阵进行并行计算。
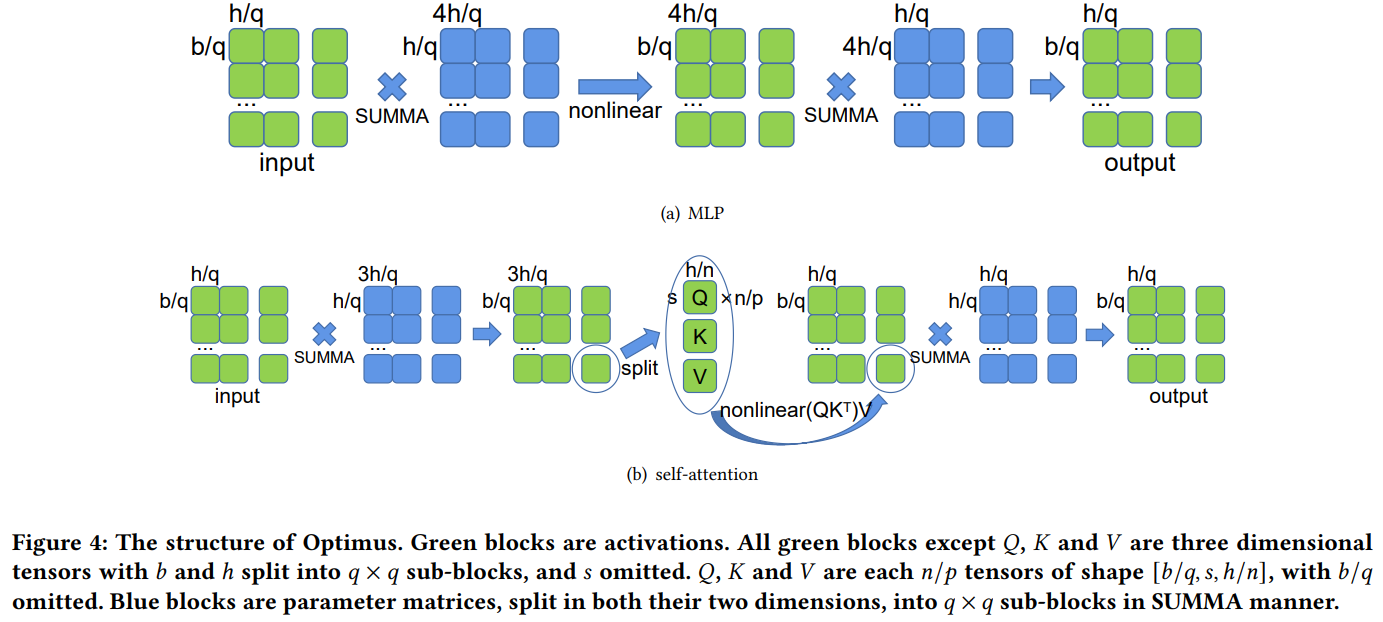
效果:每张GPU上,中间激活值变为1D TP的$\frac{1}{q^2}$,因此可以使用更大的batch size,计算量和参数量变为1D TP的$\frac{1}{q}$,但是代价是通信带宽和通信时延变大了(变为原来的3倍)
2.5D Tensor Parallel
2D TP虽然减小了激活值、计算量和参数量,但是增加了通信带宽和通信时延。对于Y=XA,2D-TP中将X和A划分为二维网格(对应$q\times q$个处理器);2.5D-TP中将X划分为三维网格,将A划分为二维网格,然后再使用SUMMA算法计算并行矩阵乘(需要$d\times q\times q$个处理器)。在d=1时,2.5D-TP退化为2D-TP,d=q时,2.5D-TP变成了3D-TP。
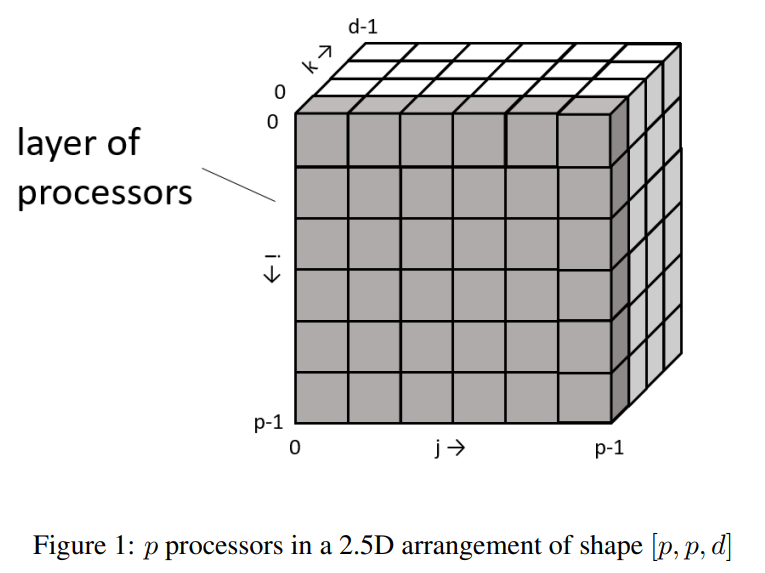
上图中,将输入X划分为d个二维网格,图中排布成了三维的结构(但是感觉排布成多个二维网格stack的形式更好?)。效果是,每张GPU上,中间激活值和计算量变为2D-TP的$\frac{1}{d}$,参数量没变,通信带宽减小了,通信时延没变。
3D Tensor Paralllel
类似的,对于Y=XA,3D-TP中将A和X划分为三维网格(对应$q \times q \times q$个处理器),计算量、参数量、中间激活都变成了2D-TP的$\frac{1}{q}$,通信带宽变为2D-TP的$\frac{1}{q^2}$,通信延时与2D-TP相同。
序列并行
原来Transformer的Attention部分的计算复杂度是输入序列长度的二次方,因此一般输入序列长度不会太长。序列并行没有在算法角度上改变Attention的计算,Attention的输入仍然是是[b, s, h]的形状,序列并行在s维度上切分,将每一个输入分块放在一个GPU上,在计算过程中进行通信。经过s维度的切分,这样每个GPU上Attention的输入就变成了[b, s/N, h],因此输入序列可以很长。
more reading:
Colossal-SP
原来Attention的计算为:$Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$,Colossal-SP中将Attention变成了分布式环境下的Ring Self-Attention,具体过程为(下面是单头的示意图,每个Q、K、V大小为[b, s/n, h/a]):
(一开始的输入已经在s维度进行了切分,每张卡的输入为[b, s/n, h])
在计算$QK^T$的过程中,通过Ring的方式传递K,因此每个GPU上分块的Q可以看见所有的K
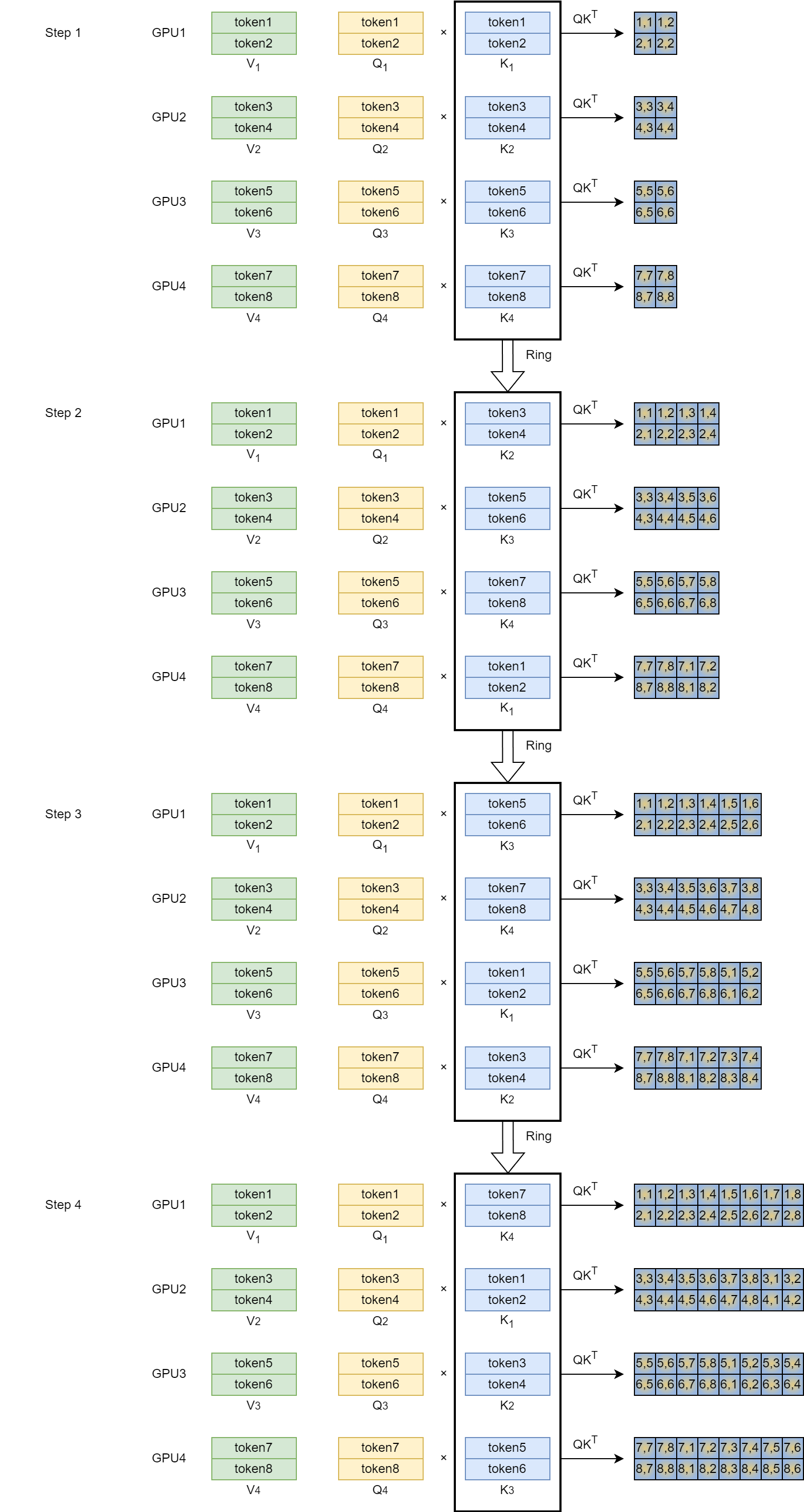
在计算$attn_score \times V$的过程中,通过Ring的方式传递V,类似上面的过程
需要注意的有以下几点:
- Colossal-SP针对的是encoder-only架构的的SP并行,针对decoder-only架构,因为attn_score后还要加上一个mask,比如上图GPU1在step4阶段需要mask掉 attn_score[1, 2:8]和 attn_score[2, 3:8],mask矩阵较大;而GPU4只需要mask掉attn_score[7,8]即可,被mask掉的部分,$Q_iK_j^T$即使算了也是白算,所以这些部分可能不会实际进行计算,后面直接加上一份负无穷大的数,这样就导致不同GPU计算负载不均衡,前面mask多的部分计算少,后面mask少的部分计算多。
在该论文中,除了提出了Colossal-SP,还针对FFN部分进行了分析。
- 原来Megatron-LM的TP并行中,输入的是完整的中间激活[b, s, h],对Linear的权重进行了切分。
- 当序列s比较长的时候,可能输入的中间激活占用显存比权重更大。因此,论文中对输入的中间激活也在s维度进行切分,每张卡上FFN部分的输入的中间激活形状为[b, s/n, h],此时需要每张卡上保留完成的Linear权重
到底哪个更省显存,需要根据模型结构、序列长度等进行计算,比如GPT类的FFN和Llama类的FFN结构就稍有区别,但总的来说就是将FFN部分的激活占用的显存和参数占用的显存加在一起,比一下,也不复杂。论文中举了一个GPT FFN的例子,结论是当$bs \gt 32h$时,序列并行更省显存(这里符号表示与论文不一样,参考文章开头的描述)
Megatron-SP
Colossal-SP与Megatron-SP都是将[b, s, h]的输入在s维度进行切分,但是其实是解决的不同的问题。Colossal-SP通过SP切分,解决了在分布式环境下训练超长序列的问题,解决方式是s维度切分+Ring通信。Megatron-SP通过SP切分,解决了每张卡上Transformer Block中LN和Dropout都要保留一份完整的[b, s, h]的输入的问题,解决方式是s维度切分+修改通信方式,具体过程为:(上图是Megatron-TP,下图是Megatron-SP)

将LN后面的通信从$f$替换为$g$
- Megatron-TP中,LN之前是完整的[b, s, h]激活,经过LN之后仍然是完整的[b, s, h]激活,正好输入到Self-Attention中。反向过程中,每张卡都有对输入激活的完整的un-reduced梯度,需要先all-reduce平均后,才能继续向前进行反向传播
- Megatron-SP中,LN之前是沿s维度切分的[b, s/n, h]激活,经过LN之后,需要先经过all-gather通信,每张卡拿到完整的[b, s, h]激活,才能输入到Self-Attention中。反向过程中,每张卡都有完整的un-reduced梯度,需要先经过reduce-scatter,每张卡拿到对不完整的输入激活对应的不完整的reduced梯度,才能继续向前反向传播
将Dropout前面的通信从$\bar{f}$替换为$\bar{g}$
- Megatron-TP中,Dropout之前是每张卡上MHA部分的计算的输出激活,前向过程中需要先对不同卡上该输入激活进行一个all-reduce平均,然后再Dropout。反向过程中,梯度在FFN部分的$f$进行过一次all-reduce,再经过LN和Dropout后,此时还没有必要使得对MHA输入的梯度都相同,所以直接$\bar{f}$的反向是no op
- Megatron-SP中,经过TP切分之后的MHA和FFN,每张卡都有一份完整的、un-reduced输入激活,进行一次reduce-scatter正好可以使得中间激活恢复到每张卡上只有一份不完整的reduced激活。反向过程中,MHA和FFN部分的反向需要使用到对输出的完整的梯度,此时每张卡上只有一块不完整的梯度,所以要进行一次all-gather拿到对输出激活的完整的梯度。
$f$:FWD=no_operation, BWD=all-reduce
$\bar{f}$:FWD=all-reduce, BWD=no_operation
$g$:FWD=all-gather, BWD=reduce-scatter
$\bar{g}$:FWD=reduce-scatter, BWD=all-gather
需要说明的有两点:
- Megatron-SP需要配合Megatron-TP使用,Megatron-TP在MHA和FFN之前仍然需要使用完整的输入激活,但是Colossal-SP可以使用序列切分之后的不完整的输入进行Self-Attention的计算(Ring Self-Attention)
- Megatron-SP的通信量与Megatron-TP的参数量和通信量相同,中间激活减少,计算量也减少
该论文中还提到一点优化,叫做selective re-compute,就是对于那些占据大量中间激活、但是计算量小的部分,这些部分可以开启重计算(之前全部重计算叫做full re-compute)。比如Transformer block中,$QK^T$矩阵乘法,softmax,softmax dropout,attn_score和V的矩阵乘法,这是一个连续的部分,占用激活多,但是计算量不大,这部分可以在训练过程中进行重计算,比如实际训练中,论文中提到GPT-3的例子,这样开启selective re-compute后,节省了70%的显存,但是只增加了2.7%的FLOPs,看起来很划算。
Ulysses
Ulysses可以认为是对前面Colossal-SP的改进,Colossal-SP中在序列s的维度进行了切分,在计算Attention的时候,采用了Ring Self-Attention方法,假如有N个GPU,那么需要进行N-1次的Ring,每次单卡通信量为$[b, \frac{s}{N}, \frac{h}{a}] \times a$个头,因此单卡每次前向需要的通信量为:$2(N-1) \times (b \times \frac{s}{N} \times h) = 2bsh \times \frac{N-1}{N}$。Ulysses对这个通信量进行了优化,Attention部分具体过程为:
- (一开始的输入已经在s维度进行了切分,每张卡的输入为[b, s/n, h])
- 每张卡上先乘$W_Q, W_K, W_V$得到Q,K,V
- 极其注意此时$W_Q, W_K, W_V$的维度是[h, h],而Colossal-SP和Megatron-SP中$W_Q, W_K, W_V$的维度是[h, h/a]
- 也就是说,对于[b, s/n, h]的输入,Ulysses在每张卡上都保留了所有head的Q、K、V(Q、K、V的维度是[b, s/n, h]),而Colossal-SP和Megatron-SP只在每张卡上保留了该卡上对应head的Q、K、V(Q、K、V的维度是[b, s/n, h/a])
- 此时每张卡上Q、K、V的维度是[b, s/n, h],对Q、K、V在h维度上切分,一共a个头,正好切成a份(这个部分没有在图虫表示),后续每张卡上都会进行$\frac{a}{N}$个头Attention的计算(比如下图中a=8,N=4,每张卡上进行2个头的Attention的计算)。这个操作也是很好理解,因为本来QKV就应该划分成多头,每个头计算一部分。
- 进行All-to-All通信。刚才在每张卡上都对QKV按头进行了切分,现在将每张卡上QKV对应head1、head2的部分(颜色最浅)发送到GPU1,将每张卡上QKV对应head3、head4的部分发送到GPU2,将每张卡上QKV对应head5、head6的部分发送到GPU3,将每张卡上QKV对应head7、head8的部分(颜色最深)发送到GPU4。
- 每张卡上进行多头注意力的计算,就像Megatron-TP那样
- 算完了多头注意力,然后再All-to-All通信,将计算结果物归原主

分析一下单卡通信量,每个Q、K、V的大小是[b, s/n, h],需要发送给其他GPU的部分是其中的$\frac{N-1}{N}$,通信量=$3 \times (b \times \frac{s}{N} \times h) \times \frac{N-1}{N} = 3bh \times \frac{s}{N} \times \frac{N-1}{N} = 2bsh \times \frac{N-1}{N} \times \frac{3}{2N}$,从复杂度上看是Colossal-SP通信量的$\frac{1}{N}$。而且注意到一点,如果序列长度翻倍,那么只要GPU数量也翻倍,则通信量不变。
还有两点需要说明:
Ulysses可以和ZeRO-3一起使用,因为Ulysses中通信的都是中间激活值,每张卡上Wq、Wk、Wv、Wo及其梯度和optimizer_states可以切分放在不同的DP上,进一步节省显存
Ulysses的一个缺点是,每张卡上负责$\frac{a}{N}$个head的计算,每个head可以使用FA进行单卡优化,但是如果模型使用MQA、GQA等方式,头数a本来就不大,也就限制了N的大小
参考:
Ring-Attention
Ring-Attention的提出还是在Colossal-SP这篇论文中,此时Ring-Attention还是使用two-pass的方式,先Ring K,再Ring V。在后续的论文中,基于FA online-softmax的思路(或者直接调用flash-attention的接口),成功将two-pass的方式优化成one-pass的方式,一次Ring就可以计算最后的输出$O$。还有一个优化点是针对Ring-Attention由于casual mask导致的计算负载不均衡问题。一个优秀的开源实现是ring attention + flash attention:超长上下文之路,这里基本按照该实现的思路,简单描述一下过程。

首先还是针对[b, s, h]的输入,在s维度上进行切分,每个GPU上分别有一个$V_i, Q_i, K_i$分块,然后使用flash-attention进行计算,得到一个局部的$O_i$,以及flash-attention函数特有的一个返回值$lse_i$
关于flash-attention和这个返回值$lse$,可以查看flash_attention简要笔记中的记录,简单来说,$lse=log[\sum_j e^{S_{ij}-rowmax(S_{ij})}]$,其中$S_{ij}=Q_i\times K_j^T$
对于每个头,每个step都会有:
每个GPU上有一个$Q_i, K_i, V_i$分块,基于flash-attention算出的局部的输出$O_i$(记为$block_O_i$),和一个$lse_i$(记为$block_lse_i$或者$new_lse_i$)
(除了第一个step)还有全局的、未修正的输出$O_i$和$lse_i$
此时对全局的、未修正的输出$O_i$和$lse_i$进行修正,具体修正公式见上图的step2(第一个下标表示rank id,第二个下标(if have)表示step),这里以GPU1为例,此时进行$Q_1, K_2, V_2$的flash-attention计算,其中$S_{12}=Q_1K_2^T$
实际代码中没有采用这种修正方式,进行了一些优化,具体介绍见:improve readability and potential numerical stability of
outandlsein_update_out_and_lseby refactoring their computational expressions. #34(除了最后一个step)在每个step的最后,会进行Ring KV的通信
还有针对由于mask导致的计算负载不均衡的问题,采用stripped ring-attention或者zigzag ring-attention的方法,该实现中为了调用flash-attention的接口,使用zigzag ring-attention的方法,这里解释一下(或者可以见USP: A Unified Sequence Parallelism Approach for Long Context Generative AI中的load balance partition):
如果使用stripped ring-attention,比如GPU0上的Q分块是$Q_0, Q_4, Q_8, Q_{12}$,K分块是$K_0, K_4, K_8, K_{12}$,然后在Ring的过程中,还可能与GPU2的K分块$K_2, K_6, K_{10}, K_{14}$算attention,比如$Q_0, Q_4, Q_8, Q_{12}$与$K_2, K_6, K_{10}, K_{14}$算attention,$S_{ij}=Q_iK_j^T$需要进行mask的部分是:
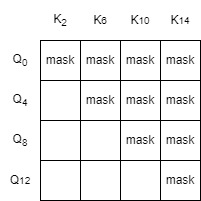
注意到Q和K都是分块,每个分块有若干行向量,标准attention的mask是上三角矩阵,但是上面示意的mask部分是台阶形状的(比如$Q_0$的最后一个向量和$K_2$的第一个向量需要进行mask,但是转到Q的下一行,即$Q_4$,$Q_4$又不需要与$K_2$进行mask,所以mask一下就断层了),由于这个原因,就没法调用标准的flash-attention
如果使用zigzag ring-attention,比如GPU0上的Q分块是$Q_0, Q_1, Q_{14}, Q_{15}$,K分块是$K_0, K_1, K_{14}, K_{15}$,然后在Ring的过程中,还可能与GPU2的K分块$K_4, K_5, K_{10}, K_{11}$算attention,比如$Q_0, Q_1, Q_{14}, Q_{15}$与$K_4, K_5, K_{10}, K_{11}$算attention,$S_{ij}=Q_iK_j^T$需要进行mask的部分是:
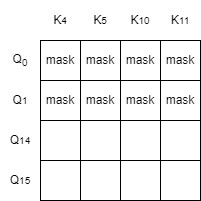
所以博客中说是一个完整的方形,因此可以直接调用flash-attention的接口了
大模型训练之序列并行双雄:DeepSpeed Ulysses & Ring-Attention中有对Ulysses和Ring-Attention的比较,,参考这篇博客,自己重新进行了理解:
- 通信量
- Ulysses单卡通信量为$2bsh \times \frac{N-1}{N} \times \frac{3}{2N}$
- Ring-Attention每个step会Ring KV,KV大小为$bsh$,需要Ring N-1次,每张卡通信量都是相同的,所以单卡通信量为$2bsh\times \frac{N-1}{N}$
- 可以看出Ulysses的通信量大约为Ring-Attention的$\frac{1}{N}$
- 通信方式:Ulysses需要All2All通信,更加复杂
- 内存使用:近似
- 其他特点:
- 模型结构的适配:Ring-Attention对头数没有要求,而Ulysses会受到头数的限制
- 输入长度的适配:Ulysses对输入长度没有要求,而Ring-Attention需要进行负载均衡
more reading:
USP(Unified Sequence Parallelism)
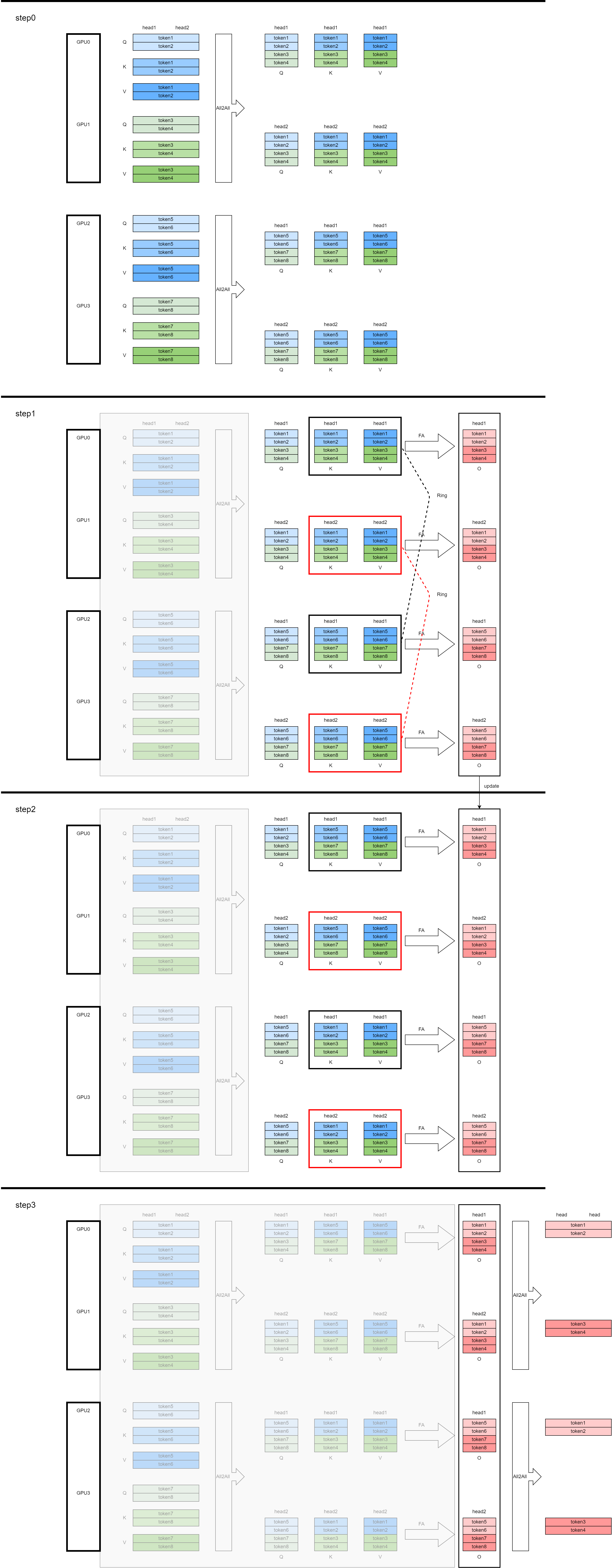
总的来说就是将Ulysses-SP和Flash-Ring-Attention结合结合起来,具体过程是:(假设一个node有2张卡,一个2个node,总的序列长度为8,头数为2)
- step0,进行Ulysses的操作,在每个节点内进行All2All通信(每个节点内部构成一个通信组,比如GPU0、GPU1构成一个通信组,GPU2和GPU3构成一个通信组,通信组内部进行All2All的通信),此时每个节点得到一份节点内部完整序列的、按头切分的QKV,
- 然后进行Flash-Ring-Attention的操作,接下来每个step中:
- 基于局部的Q、K、V,进行flash-attention的计算,如果当前不是Ring-Attention的第一个step,则对输出O要进行修正
- 如果不是Ring-Attention的最后一个step,要进行K、V的Ring通信。在图中,对位于不同GPU上的、相同head的、不同部分序列的K、V进行Ring通信,比如GPU0和GPU2、GPU1和GPU3分别构成通信组,Ring通信在通信组内进行P2P通信
- 最后(step3)再进行Ulysses的操作,将输出All2All通信,对应的token物归原主
more reading:
通过将USP用在Megatron-LM中,给出了USP加入之后4D混合并行最佳实践方案:序列并行做大模型训练,你需要知道的六件事
给出了一个USP潜在适合应用的场景,序列长度变化的SFT训练任务:LLM变长序列分布式训练迷思
USP应用在Megatron-LM中,如何做通信计算重叠来追求更极致通信优化:大模型训练优化:论反向传播中序列并行和张量并行的通信计算重叠方法
Context Parallel
Context Parallel很像(甚至就是)Ring-Attention,这里从历史发展的角度,进行一个简单的辨析:
首先说一下Sequence Parallel。一开始(2021.05)有two-pass的Colossal-SP;然后后来(2023.10)改进成了one-pass的Ring-Attention,此时的one-pass是作者基于jax框架重新实现的、对输出O的调整逻辑(比如手动更新denominator和max_score,分别对应flash-attention原始论文中的$l$和$m$);再后来(2024.02)朱小霖实现了一版开源的Ring-Attention,特点是仍然保持了one-pass的Ring-Attention,但是中间通过调用现有的flash-attention接口(会返回lse,用这个可以对输出O进行修正)避免了one-pass FA部分内部逻辑的改动(因此这个开源实现叫做ring-flash-attention),而且使用zigzag的方式实现了计算负载均衡。
然后说到Context Parallel,Context Parallel主要是针对Megatron-LM的。
一开始(22.05)Megatron-LM也提出了序列并行,这里把它叫做Megatron-SP,Megatron-SP和Colossal-SP都是针对序列维度进行切分,但是采用的不同的优化方法,Megatron-SP主要是在LN和Dropout的前面对输入在序列维度上进行切分,self-attention的前面经过All-Gather拿到了全部序列。
后来,Megatron-LM也采取了Ring-Attention的思想,原来attention之前不是要【前向All-Gather/反向Reduce-Scatter】吗,现在将这个【前向All-Gather/反向Reduce-Scatter】转换为P2P通信(比较困惑,后续需要结合代码看一下)。Megatron-LM中说CP相对于Ring-Attention的优势是(这里指的Ring-Attention,指的是Ring Attention with Blockwise Transformers for Near-Infinite Context,此处的实现,作者基于jax框架,将flash-attention重新时间并融合到Ring-Attention中):
充分利用最新开源的cuDNN flash attention kernel
tip: OSS 表示 Open Source Software
移除由于上三角mask导致的不必要计算,从而实现负载均衡
Megatron中对CP的介绍部分的原话是:
Context Parallelism (“CP”) is a parallelization scheme on the dimension of sequence length. Unlike prior SP (sequence parallelism) which only splits the sequence of Dropout and LayerNorm activations, CP partitions the network inputs and all activations along sequence dimension. With CP, all modules except attention (e.g., Linear, LayerNorm, etc.) can work as usual without any changes, because they do not have inter-token operations. As for attention, the Q (query) of each token needs to compute with the KV (key and value) of all tokens in the same sequence. Hence, CP requires additional all-gather across GPUs to collect the full sequence of KV. (计算Attention之前,要进行一次all-gather通信)Correspondingly, reduce-scatter should be applied to the activation gradients of KV in backward propagation. To reduce activation memory footprint, each GPU only stores the KV of a sequence chunk in forward and gathers KV again in backward.(为了省显存,前向all-gather拿到全部的KV后,算完attention后只保存一块KV,反向时类似重计算一样重新all-gather一次) KV communication happens between a GPU and its counterparts in other TP groups. The all-gather and reduce-scatter are transformed to point-to-point communications in ring topology under the hood.(all-gather和reduce-scatter) Exchanging KV also can leverage MQA/GQA to reduce communication volumes, as they only have one or few attention heads for KV.
而且附了一张图:
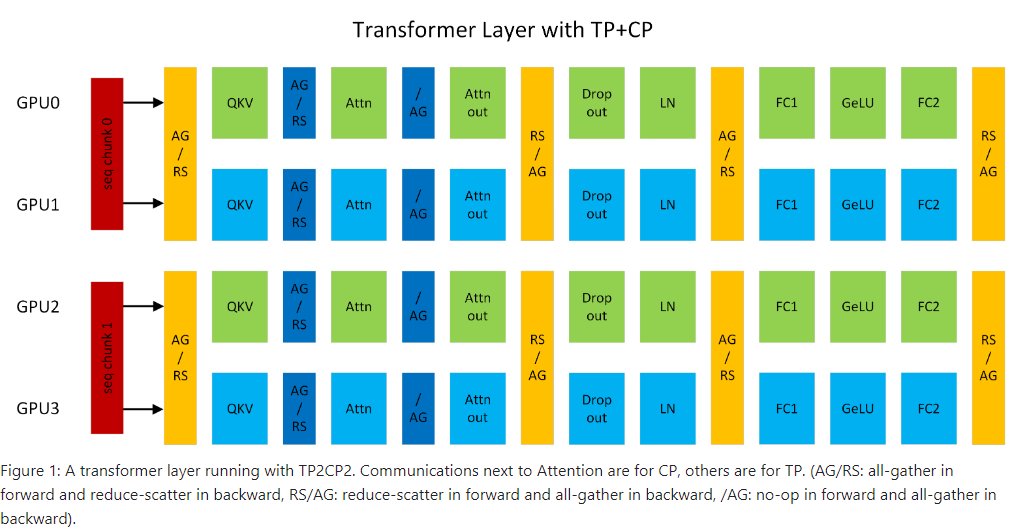
意思是在TP2CP2的情况下,GPU0和GPU1、GPU2和GPU3分别构成两个TP group,GPU0和GPU2、GPU1和GPU3分别构成两个CP group,按序列切分的输入经过第一个AG/RS,在一个TP group上得到了一个half的输入,然后得到QKV。接下来进行CP的通信操作,这里在CP group内部进行all-gather通信,后面的过程基本与原来相同。
(橙色的通信都是TP的,深蓝色的通信是CP的)
在具体实现上,Megaron-LM中设置好CP的相关通信组cp_group之类的,然后将该cp_group传入到Megatron-LM调用的TransformerEngine中;在TransformerEngine中,如果使用flash-attention,调用的是
attn_forward_func_with_cp,内部根据cp通信方式的不同,又进一步调用了以下实现:如果
cp_comm_type=='p2p',则调用AttnFuncWithCPAndKVP2P- 内部通信调用的是
torch.distributed.P2POp
- 内部通信调用的是
如果
cp_comm_type=='all_gather',则调用AttnFuncWithCPAndKVAllGather- 内部通信调用的是
torch.distributed.all_gather_into_tensor
在llama3 3.3.2节 Context parallelism for long sequences 中,首先给出了负载均衡的办法,类似于上面朱小霖开源Ring-Attention中的zigzag方式,然后原来Ring-Attention中用的是P2P通信(可以通信计算重叠),现在改成先All-Gather拿来K和V,原因有二:
- it is easier and more flexible to support different types of attention masks in all-gather based CP attention, such as the document mask
- 由于使用了GQA,通信的K和V都比原来小了很多,通信时延也变小了
- 内部通信调用的是
如果
cp_comm_type=='a2a',则调用AttnFuncWithCPAndKVPA2A类似Ulysses-SP,没有Ring的操作
more reading:
专家并行Expert Parallel
进入到具体模型结构之前,首先要明确一个概念:MoE是在多个GPU上共享的,或者说,非MoE的部分像数据并行一样在多个GPU上有一份模型的replica(一份复制),但是MoE的部分是这多个GPU共享的,即每个GPU上放几个专家(注意这个不是专家并行EP,EP指的是一个专家放在多个GPU上),这些专家共同组成一个MoE结构。MoE在算法方面的改进更多一些,本文也会简单介绍,但是更多侧重还在于工程角度和具体过程。
MoE基本范式是:(图中红色表示输入输出,紫色表示中间变量,黑色表示通信和操作)
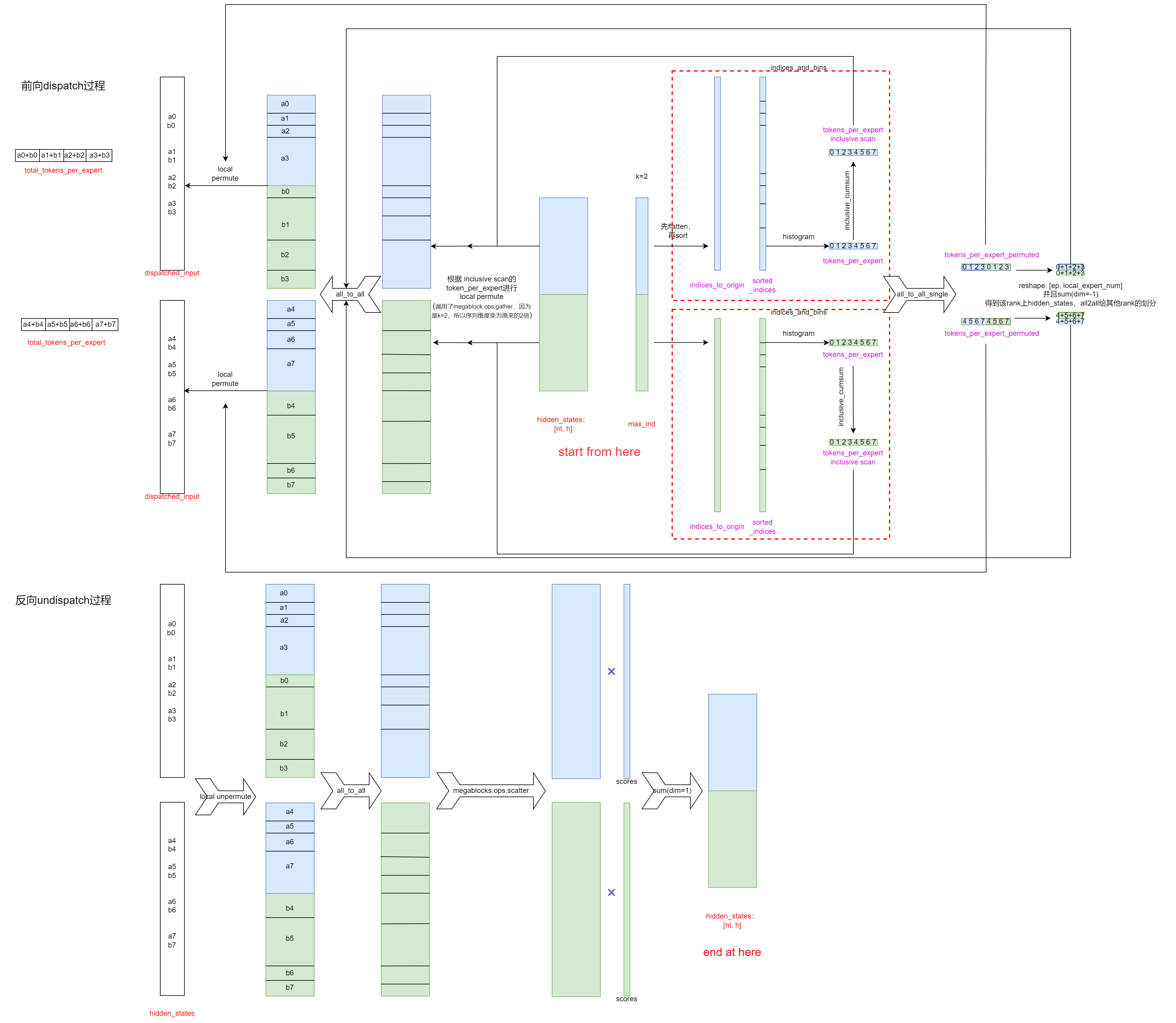
- gating:[b, s, h]的输入先经过gating,输出是[b, s, e],表示每个token分配到每个专家的概率,其中e指的是专家数量(实际上就一个linear+softmax的过程)。然后取topk专家,输出是[b, s, k],表示每个token根据上面计算的概率选择了概率最大的k个专家,[b, s, k]中记录的是选择的专家的index
- dispatch(上图中上半部分):将[b, s, h]的输入tokens根据[b, s, k]的专家index,路由到特定的专家
- 需要注意的一点是,原来输入是batched,首先经过一次all2all通信,将token发送到对应专家所在的GPU上;如果一个GPU上有多个专家,那么还要进行一个本地的重排,使得发送给一个专家的tokens batch到一起
- 专家计算
- undispatch(上图中下半部分):dispatch的逆过程
Gshard
这是首次将MoE引入到Transformer的工作,将Encoder中的那一个FFN替换为一个MoE,相当于就是在FFN前面加了一个gating来进行路由选择(top2),而且每间隔一层来进行MoE的替换(比如一层MoE,一层FFN,这样交替循环)
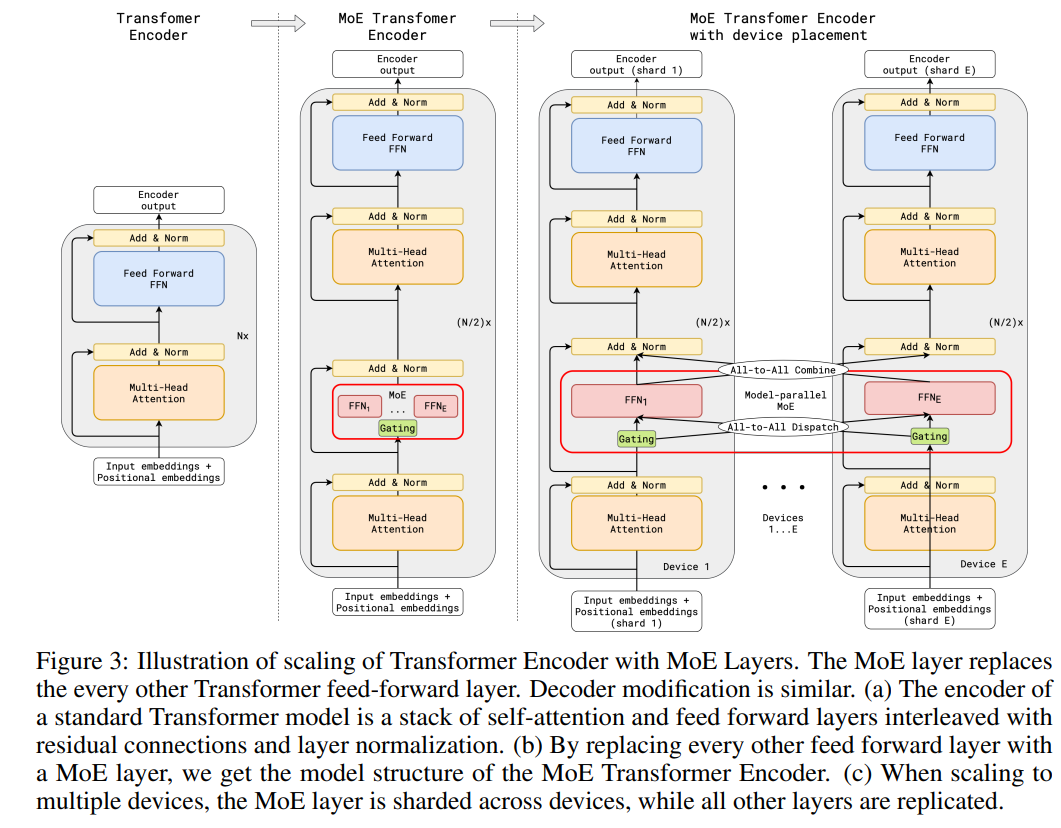
Switch Transformer
Switch Transformer主要针对Gshard进行了三点改进:
简化路由:从原来top2简化到top1,也能保证模型的质量
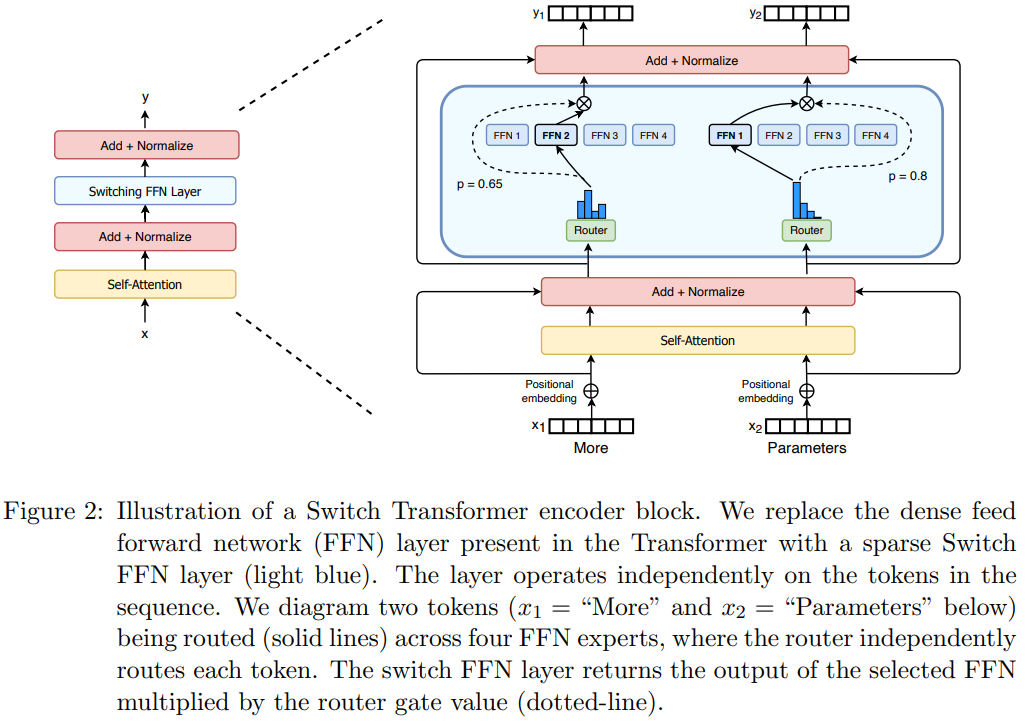
高效路由:
专家容量(expert capacity)和容量因子(capacity factor):由于Switch Transformer是基于Mesh-TensorFlow实现的,该框架要求每个专家输入的Tensor shape是固定的,即需要提前分配好大小,但是由于动态路由,不到运行时也不知道每个专家有多少输入token。因此,干脆固定某个大小算了,这个固定的大小就叫做专家容量(expert capacity),具体来说就是$expert_capacity=capacity_factor \times \frac{tokens_per_batch}{number_of_experts}$,其中这个分数表示一个mini-batch平均分到每个专家的token数量,容量因子就是来扩大这个平均值的
如果容量因子太大,则提前分配的专家容量越大,其中需要padding的token越多,增加了无效计算
如果容量因子太小,如果某个token分配到某个专家,但是该专家的输入缓冲区已经满了,只能将该token丢弃,然后最后残差连接加回去,比如说像下面这个图(图中采取top2,但是Switch Transformer采取top1,这里只是为了说明drop token的例子),token7分配到expert2和expert3,但是这两个专家的输入缓冲已经满了,只能丢弃,然后残差跳过MoE连接到后续非MoE部分,或者说相当于MoE部分对该token的输出是0
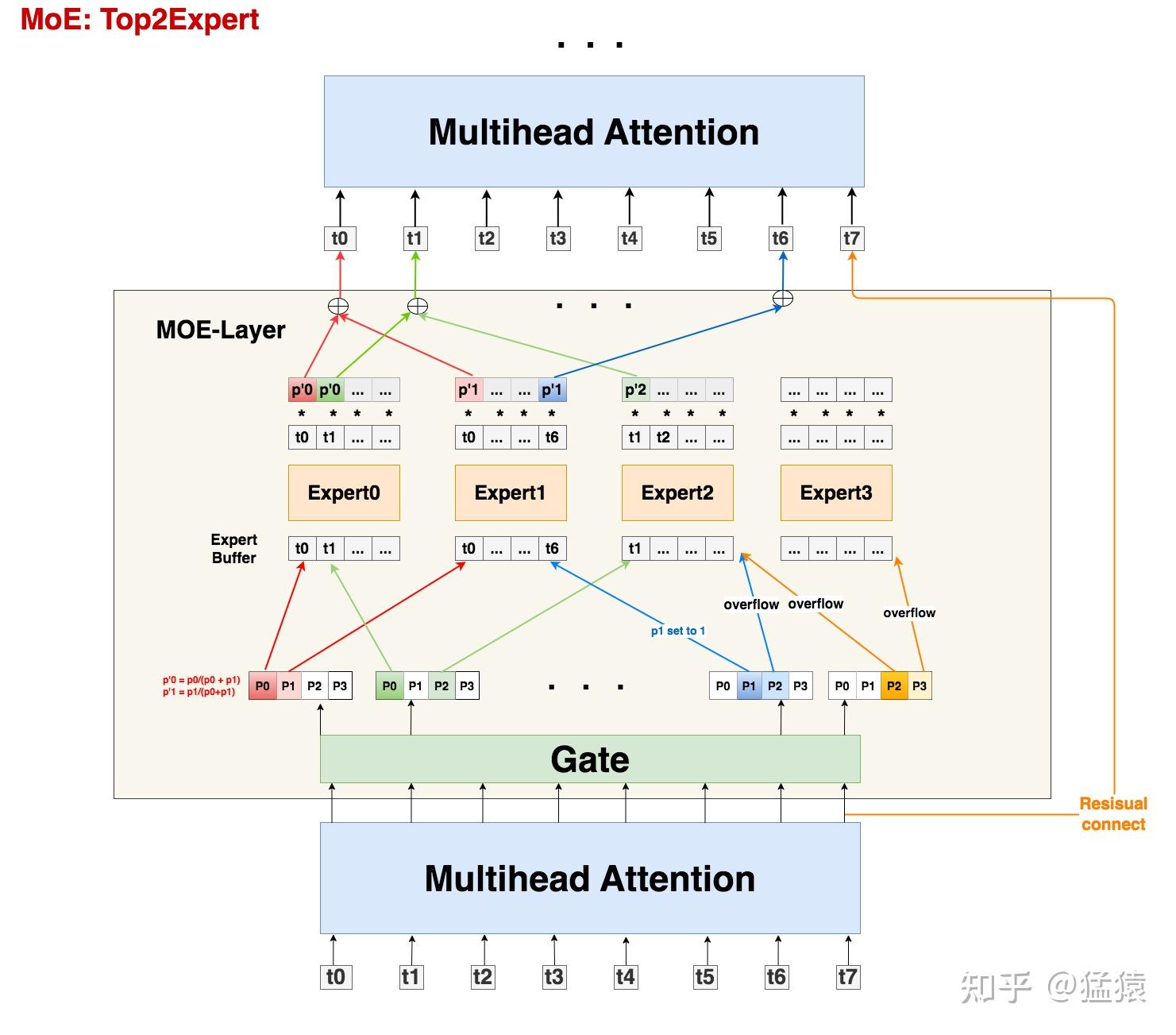
Load balance loss:由于token进行动态路由,可能有的专家要处理很多token,有的专家处理很少token,为了负载均衡,提高模型训练和推理效果和性能,最好做到token在不同专家之间分配大致相同,添加的$P_i$一项只是为了保证loss可以求导(前面那些部分无法求导)

还提出了四条有助于提升预训练和微调稳定性的技巧,由于本文更多关注于工程角度和具体流程,这里省略
FastMoE
该论文的创新点:
- 之前分布式MoE主要是基于TPU和Mesh-Tensorflow框架,FastMoE基于GPU和PyTorch框架,实现了EP并行
- 工程优化:
- 将专家模块进行抽象,使得任意网络可以作为专家
- 将一个GPU上多个专家的计算过程整合为一个batched_gemm
- 在all2all通信token之前,先all2all通信一下token的数量和大小,由此来动态分配空间
DeepSpeed-MoE
该论文对Switch Transformer有两点改进:
提出了新的MoE结构(叫做PR-MoE,金字塔MoE),变化有两处:
观察到在模型靠后的层使用MoE比模型前面层使用MoE的算法效果更好,所以随着模型层数增加,后面的层使用更多的专家,这样同时也减小吗MoE的显存
观察到top2 gating比top1 gating算法效果好,因此固定一个expert,然后剩下再进行top1 gating,这样路由过程与Switch Transformer相同,但是达到了top2 gating的效果
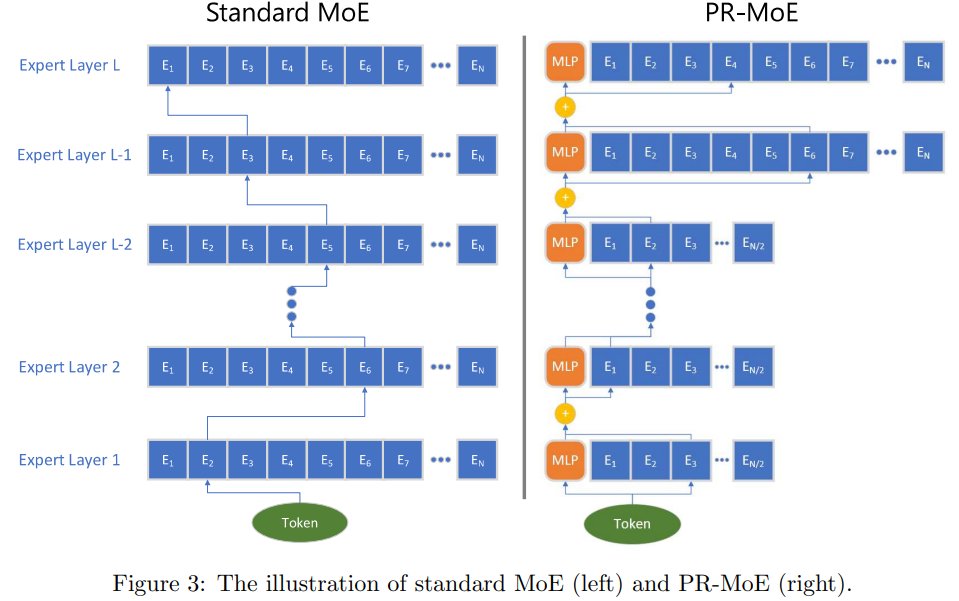
从推理角度改进了模型的并行方法,推理场景主要特征是batch_size比较小,所以可能不适合训练场景
TUTEL
静态的策略不能满足MoE的动态特性(即专家的输入缓冲是固定大小的,但是训练过程中专家处理token数量是不固定的,有可能drop token损失精度,有可能padding浪费计算资源)
Tutel允许在每次训练迭代中,设置不同的expert_capacity,所以Tutel可以保证不drop tokens,但是没法避免zero-padding。
参考:
MoE训练论文解读之Tutel: 动态切换并行策略实现动态路由
MegaBlocks
该论文针对一个GPU上多个专家、而且没有专家容量限制(即没有drop token,没有padding,来多少token就计算多少token)的MoE场景。
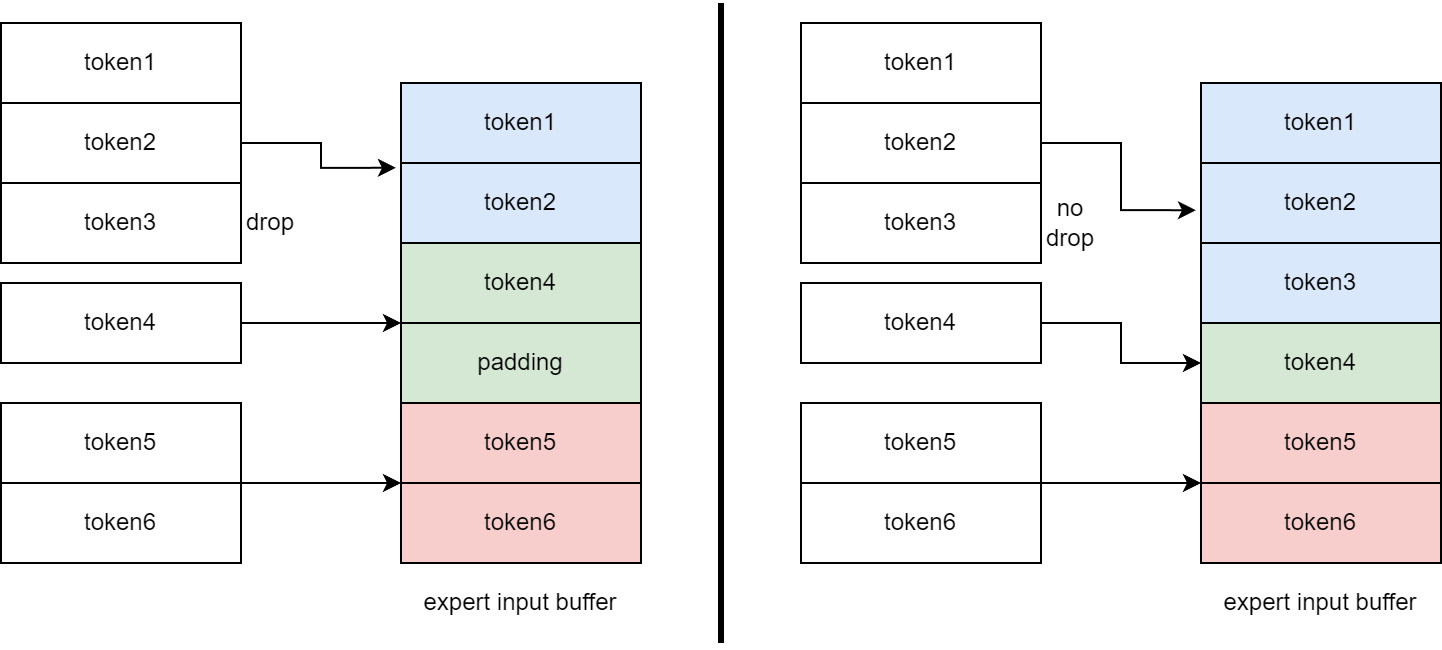
原来一个GPU上多个专家、有专家容量限制时,像左图,token3被drop,专家2的input buffer需要padding,此时输入大小都相等,可以直接调用cutlass中的batched gemm操作。现在一个GPU上多个专家、没有专家容量限制时,像右图,每个专家的input buffer大小不同,
cutlass中的grouped gemm操作需要输入维度大小相同,Megablocks中提出了Variable Sized Grouped GEMM操作
但是该论文的一个缺陷是,该论文要求专家数量>GPU数量,但是在实际场景中往往GPU数量是更多的
评测指标
MFU+HFU共同衡量了某一模型实现对某种芯片计算性能的利用情况:
- MFU(Model FLOPs Utilization):模型算力利用率,指模型一次前反向计算消耗的矩阵算力与机器算力的比值
- 实际计算中,$MFU=\frac{每token模型的FLOPs \times 每秒的token数量}{机器峰值FLOPs}$
- HFU(Hardware FLOPs Utlization):硬件算力利用率,指考虑重计算后,模型一次前反向计算消耗的矩阵算力与机器算力的比值
还有一点需要说明,MoE的MFU一般相对较低
更新
发现了更加优质的系列好文:
- 大规模分布式 AI 模型训练系列——数据并行
- 大规模分布式 AI 模型训练系列——流水线并行
- 大规模分布式 AI 模型训练系列——张量并行
- 大规模分布式 AI 模型训练系列——序列并行
- 大规模分布式 AI 模型训练系列——专家并行
llama3 pipeline:https://mp.weixin.qq.com/s/1syPf8XNQfgk7mClMDSqhw