[toc]
1.自动微分¶
1.1 初步封装¶
首先我们考虑函数的自动微分。函数是这样的:$y=f(x), l=L(y)$,其中x表示输入,y是中间变量,L相当于是损失函数,l是损失函数计算出来的loss,大致模拟神经网络的结构。
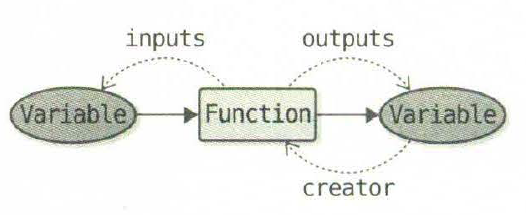
从中可以抽象出两个部分,输入/输出的变量Variable,和中间计算的函数Function。
首先我们对Variable进行初步封装:
1
2
3
| class Variable:
def __init__(self, data):
self.data = data # data是一个numpy的ndarray
|
然后对Function进行初步封装:
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Function: # 基类
def __call__(self, input): # __call__方法将Variable类型的input中数据成员data取出来进行计算,计算完成后再返回Vaiabel
x = input.data
y = self.forward(x)
output = Variable(y)
return output
def forward(self, x): # 实际进行计算的函数
raise NotImplementError()
class Square(Function):
def forward(self, x):
return x ** 2
|
1.2 反向传播¶

观察前向传播和反向传播的流程图,可以看出Variable和Function中前向和反向中存在一定的对应关系,即Variable中需要同时保存数据成员和其激活值,Function中需要同时有forward和backward过程,因此可以拓展Variable和Function类:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Variable:
def __init__(self, data):
self.data = data
self.grad = None
class Function:
def __call__(self, input):
x = input.data
y = self.forward(x)
output = Variable(y)
self.input = input
return output
def forward(self, x):
raise NotImplementError()
def backward(self, gy): # gy是loss值l对y的导数值,backward中实现以下y对x的导数,返回相乘的结果
raise NotImplementError()
class Exp(Function):
def forward(self, x):
y = np.exp(x)
return y
def backward(self, gy):
x = self.input.data
gx = np.exp(x) * gy
return gx
x = Variable(np.array(0.5))
F = Exp()
y = F(x)
# 但是这样只能手动实现反向传播
y.grad = np.array(1.0)
x.grad = F.backward(y.grad)
|
1.3 自动反向传播¶
为了实现反向传播的自动化,一个思路是使用列表记录一下函数执行的顺序(但是对于有分支或多次使用同一个变量的计算图,需要使用Wengert列表(或者叫tape))。
另一个思路是将Variable分为两种类型,一种是用户给出的,另一种是由某个Function产生的,因此可以在Variable中记录其creator;在Function运行时实际执行的过程中,此时来记录局部的变量的creator信息,因为这个“连接”的信息是在forward前向传播的过程中记录,因此这种方式也称为Define-by-Run,所构造的计算图也称为动态计算图。
比如,对于例子$y=f(x)$而言,已知$\frac{dl}{dy}$,需要求出$\frac{dl}{dx}$。计算过程是:当前可以拿到输出Variable $y$,也可以产生这个Variable的Function $f=y.creator$,然后根据$f$获取其输入Variable $x=f.input$,就可以计算出x的梯度$x.grad=\frac{dl}{dy} \times \frac{dy}{dx} = f.backward(y.grad)$。这个计算过程是相同的,可以实现程序控制的自动反向传播,因此放在Variable类中,可以递归的来进行计算,也可以转换成迭代的方法进行计算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| class Variable:
def __init__(self, data):
if data is not None:
if not isinstance(data, np.ndarray): # data should be np.ndarray type
raise TypeError("{} is not supported".format(type(data)))
self.data = data
self.grad = None
self.creator = None
def set_creator(self, func):
self.creator = func
def backward(self):
if self.grad is None:
self.grad = np.ones_like(self.data)
funcs = [self.creator]
while funcs:
f = funcs.pop(); # 因为现在针对的是函数的自动求导,所以funcs中总是只有一个元素
x, y = f.input, f.output
x.grad = f.backward(y.grad)
if x.creator is not None:
funcs.append(x.creator)
'''
# 递归版本
f = self.creator
if f is not None:
x = f.input
x.grad = f.backward(self.grad)
x.backward()
'''
def as_array(x):
return np.array(x) if np.isscalar(x) else x
class Function:
def __call__(self, input):
x = input.data
y = self.forward(x)
output = Variable(as_array(y)) # y经过forward之后未必是ndarray,比如x=np.array(1.0), y = x**2之后y是np.float64类型
output.set_creator(self) # output保存creator信息
self.input = input
self.output = output
return output
def forward(self, x):
raise NotImplementedError()
def backward(self, gy):
raise NotImplementedError()
class Exp(Function):
def forward(self, x):
return np.exp(x)
def backward(self, gy):
x = self.input.data
return np.exp(x) * gy
def exp(x):
return Exp()(x)
x = Variable(np.array(0.5))
y = exp(exp(x))
y.backward()
print(x.grad)
|
2.计算图的自动微分¶
2.1 多输入、多输出的Function实现¶
某些Function的输入可能有多个,比如Add,输出也可能有多个,比如separate,此时可以使用可变长参数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| def as_array(x):
return np.array(x) if np.isscalar(x) else x
class Function:
def __call__(self, *inputs): # 针对多个输入的可变长参数
xs = [x.data for x in inputs]
ys = self.forward(*xs) # 这里可以将xs整个列表传给forward,也可以将xs列表解包之后传给forward,分别对应的forward形参的不同形式,后一种形式更为直观和易用一些
if not isinstance(ys, tuple): # ys需要是tuple类型
ys = (ys, )
# ys = self.forward(xs)
outputs = [Variable(as_array(y)) for y in ys]
for output in outputs:
output.set_creator(self)
self.inputs = inputs
self.outputs = outputs
return outputs if len(outputs) > 1 else outputs[0]
def forward(self, x):
raise NotImplementedError()
def backward(self, gy):
raise NotImplementedError()
class Add(Function): # 多个输入,一个输出
def forward(self, x0, x1):
return x0 + x1
'''
def forward(self, xs): # xs是一个列表
x0, x1 = xs
return (x0 + x1, )
'''
def backward(self, gy): # 针对多个输入,要返回多个偏导数
return gy, gy
def add(x0, x1):
return Add()(x0, x1)
class Square(Function):
def forward(self, x):
return x ** 2
def backward(self, gy):
x = self.inputs[0].data
return 2 * x * gy
def square()
|
如果某个Function的输入是多个,那么此时输出y就应该对每个输入求偏导数,Function中backward可能返回多个偏导数,此时Variable中的backward也应该进行一些修改:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Variable:
def __init__(self, data):
if data is not None:
if not isinstance(data, np.ndarray):
raise TypeError('{} is not supported'.format(type(data)))
self.data = data
self.grad = None
self.creator = None
def set_creator(self, func):
self.creator = func
def cleargrad(self):
self.grad = None
def backward(self):
if self.grad is None:
self.grad = np.ones_like(self.data)
funcs = [self.creator]
while funcs:
f = funcs.pop() # Bug:这里需要修改
gys = [output.grad for output in f.outputs] # f的输出可能有多个
gxs = f.backward(*gys)
if not isinstance(gxs, tuple):
gxs = (gxs, )
for x, gx in zip(f.inputs, gxs):
if x.grad is None:
x.grad = gx
else:
x.grad = g.grad + gx # x.grad += gx是inplace操作
if x.creator is not None:
funcs.append(x.creator)
|
2.2 计算图的反向传播¶
为了实现反向传播,主要有两种思路。一种是对计算图进行一个拓扑排序,然后逆序进行反向传播。另一种是bfs的思路,记录一下当前Function和Variable是在哪一个level上,先取出后面level的进行反向传播。
这里采用第二种思路:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
| import heapq
import numpy as np
import weakref
class Variable:
def __init__(self, data):
if data is not None:
if not isinstance(data, np.ndarray):
raise TypeError('{} is not supported'.format(type(data)))
self.data = data
self.grad = None
self.creator = None
self.generation = 0
def set_creator(self, func):
self.creator = func
self.generation = func.generation + 1 # Variable的generation是其creator的generation-1
def cleargrad(self):
self.grad = None
def backward(self):
if self.grad is None:
self.grad = np.ones_like(self.data)
funcs = [self.creator]
heapq.heapify(funcs)
seen_set = set()
while funcs:
f = heapq.heappop(funcs) # 使用最大堆,每次弹出最大generation的creator
# print(f.generation)
for input in [input for input in f.inputs if input.creator is not None]:
if input.creator in seen_set:
continue
heapq.heappush(funcs, input.creator)
seen_set.add(input.creator)
gys = [output.grad for output in f.outputs]
gxs = f.backward(*gys)
if not isinstance(gxs, tuple):
gxs = (gxs, )
for x, gx in zip(f.inputs, gxs):
if x.grad is None:
x.grad = gx
else:
x.grad = x.grad + gx # x.grad += gx是inplace操作
def as_array(x):
return np.array(x) if np.isscalar(x) else x
class Function:
def __call__(self, *inputs): # 针对多个输入的可变长参数
xs = [x.data for x in inputs]
ys = self.forward(*xs) # 这里可以将xs整个列表传给forward,也可以将xs列表解包之后传给forward,分别对应的forward形参的不同形式,后一种形式更为直观和易用一些
if not isinstance(ys, tuple): # ys需要是tuple类型
ys = (ys, )
# ys = self.forward(xs)
outputs = [Variable(as_array(y)) for y in ys]
self.generation = max([x.generation for x in inputs]) # Function的generation是其多个输入中最大的generation
for output in outputs:
output.set_creator(self)
self.inputs = inputs
self.outputs = [output for output in outputs]
# self.outputs = outputs
return outputs if len(outputs) > 1 else outputs[0]
def __lt__(self, func): # 自定义排序,便于进行堆排序
return -self.generation < -func.generation # 因为heapq只能实现小根堆
def forward(self, x):
raise NotImplementedError()
def backward(self, gy):
raise NotImplementedError()
class Square(Function):
def forward(self, x):
return x ** 2
def backward(self, gy):
x = self.inputs[0].data
return 2 * x * gy
def square(x):
return Square()(x)
class Add(Function): # 多个输入,一个输出
def forward(self, x0, x1):
return x0 + x1
def backward(self, gy): # 针对多个输入,要返回多个偏导数
return gy, gy
def add(x0, x1):
return Add()(x0, x1)
x = Variable(np.array(2.0))
a = square(x)
y = add(square(square(a)), square(a))
y.backward()
print(y.data)
print(x.grad)
|
2.3 一些优化措施¶
针对循环引用的优化¶
原来Function的outputs和Variable的creator相互引用,如果这两个对象都不使用了,此时没法通过引用技术来回收内存(可以通过垃圾回收机制GC释放内存,但是使用GC推迟内存释放会导致程序整体的内存使用量增加)。因此一个优化是打破这个循环引用,将Function的outputs设置为弱引用,弱引用是在不增加引用技术的情况下对另一个对象的引用。
具体修改是第61行和第33行
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| import heapq
import numpy as np
import weakref
class Variable:
def __init__(self, data):
if data is not None:
if not isinstance(data, np.ndarray):
raise TypeError('{} is not supported'.format(type(data)))
self.data = data
self.grad = None
self.creator = None
self.generation = 0
def set_creator(self, func):
self.creator = func
self.generation = func.generation + 1 # Variable的generation是其creator的generation-1
def cleargrad(self):
self.grad = None
def backward(self, retain_grad=False):
if self.grad is None:
self.grad = np.ones_like(self.data)
funcs = [self.creator]
heapq.heapify(funcs)
seen_set = set()
while funcs:
f = heapq.heappop(funcs) # 使用最大堆,每次弹出最大generation的creator
# print(f.generation)
for input in [input for input in f.inputs if input.creator is not None]:
if input.creator in seen_set:
continue
heapq.heappush(funcs, input.creator)
seen_set.add(input.creator)
gys = [output().grad for output in f.outputs] # 如果output为弱引用,需要output()来获取其内容
gxs = f.backward(*gys)
if not isinstance(gxs, tuple):
gxs = (gxs, )
for x, gx in zip(f.inputs, gxs):
if x.grad is None:
x.grad = gx
else:
x.grad = x.grad + gx # x.grad += gx是inplace操作
if not retain_grad: # 不保留中间变量的梯度
for output in f.outputs:
output().grad = None # 最终只有一开始的input的grad保留下来
def as_array(x):
return np.array(x) if np.isscalar(x) else x
class Function:
def __call__(self, *inputs): # 针对多个输入的可变长参数
xs = [x.data for x in inputs]
ys = self.forward(*xs) # 这里可以将xs整个列表传给forward,也可以将xs列表解包之后传给forward,分别对应的forward形参的不同形式,后一种形式更为直观和易用一些
if not isinstance(ys, tuple): # ys需要是tuple类型
ys = (ys, )
# ys = self.forward(xs)
outputs = [Variable(as_array(y)) for y in ys]
self.generation = max([x.generation for x in inputs]) # Function的generation是其多个输入中最大的generation
for output in outputs:
output.set_creator(self)
self.inputs = inputs
self.outputs = [weakref.ref(output) for output in outputs] # 将Function的outputs变为弱引用,防止循环引用
# self.outputs = outputs
return outputs if len(outputs) > 1 else outputs[0]
def __lt__(self, func): # 自定义排序,便于进行堆排序
return -self.generation < -func.generation # 因为heapq只能实现小根堆
def forward(self, x):
raise NotImplementedError()
def backward(self, gy):
raise NotImplementedError()
|
减少内存占用的优化¶
不保留不必要的导数
在深度学习和神经网络的反向传播中,更新的是参数的权重,我们需要求得参数的梯度,但是中间激活值的梯度信息可以用完即弃,不需要保存到内存中,比如下图中,只需要保存$\frac{dl}{da}$这个梯度信息(红色部分),其他的梯度信息都不需要保存到内存中。

快速切换训练阶段和推理阶段¶
一种方式是直接使用if语句进行判断enable_backprop的值;另一种更好的方法是使用with语句实现临时的状态切换。具体而言,使用contextlib模块下的装饰器@contextlib.contextmanager修饰一个函数(比如using_config),当进入到with块的作用域时,首先调用预处理的代码(修饰函数中yield之前是预处理的代码),当离开with块的作用域时,调用后处理的代码(yield之后是后处理的代码)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| import contextlib
class Config:
enable_backprop = True
@contextlib.contextmanager
def using_config(name, value):
old_value = getattr(Config, name)
setattr(Config, name, value)
try:
yield
finally:
setattr(Config, name, old_value)
def no_grad():
return using_config('enable_backprop', False)
# example: y = x^2, with only forward
with no_grad():
x = Variable(np.array(2.0))
y = square(x)
|
对Variable的拓展和完善¶
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| class Variable:
def __init__(self, data, name=None):
if data is not None:
if not isinstance(data, np.ndarray):
raise TypeError('{} is not supported'.format(type(data)))
self.data = data
self.grad = None
self.creator = None
self.generation = 0
self.name = name
def set_creator(self, func):
...
def cleargrad(self):
...
def backward(self, retain_grad=False):
...
@property # 使用@property装饰器进行修饰,shape方法可以作为属性(或者实例变量)被访问
def shape(self):
return self.data.shape
@property
def ndim(self):
return self.data.ndim
@property
def size(self):
return self.data.size
@property
def dtype(self):
return self.data.dtype
def __len__(self):
return len(self.data)
def __repr__(self):
if self.data is None:
return "Variable(None)"
p = str(self.data).replace('\n', '\n'+' '*9)
return "Variable(" + p + ")"
|
运算符重载
1
2
| def as_variable(obj):
return obj if isinstance(obj, Variable) else Variable(obj)
|


